 1.Dla jakiego parametru m funkcja liniowa jest rosnąca ? f(x)=(m²−6)x+2
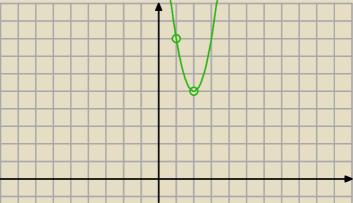
2.Dana jest funkcja kwadratora f(x)= −x²+3x+4 podaj najmniejszą i największą wartość funkcji w
przedziale x∈<1;4>
3.Napisz wzór funkcji jeżeli wiadomo ,że w przedziale(− nieskończoność;2>jest funkcją malejącą
i dla f(2)=5 oraz f(1)=8
1.Dla jakiego parametru m funkcja liniowa jest rosnąca ? f(x)=(m²−6)x+2
2.Dana jest funkcja kwadratora f(x)= −x²+3x+4 podaj najmniejszą i największą wartość funkcji w
przedziale x∈<1;4>
3.Napisz wzór funkcji jeżeli wiadomo ,że w przedziale(− nieskończoność;2>jest funkcją malejącą
i dla f(2)=5 oraz f(1)=8
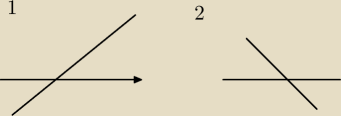 1.
Kiedy funkcja rośnie? (idzie do góry)
Wg tego co narysowałem... rośnie na pierwszym obrazku.
zeby funkcja byla rosnaca, to wspolczynnik kierunkowy funkcji "a" musi byc dodatni
skoro funkcja liniowa, to
y = ax + b
a ma być dodatnie
to
(m2−6) musi być dodatnie
Właściwie to równe zero też może być, bo prosta y=2 też jest funkcją liniową
więc
m2 − 6 > 0
Jak rozwiązać takie coś mam nadzieję, że wiesz
1.
Kiedy funkcja rośnie? (idzie do góry)
Wg tego co narysowałem... rośnie na pierwszym obrazku.
zeby funkcja byla rosnaca, to wspolczynnik kierunkowy funkcji "a" musi byc dodatni
skoro funkcja liniowa, to
y = ax + b
a ma być dodatnie
to
(m2−6) musi być dodatnie
Właściwie to równe zero też może być, bo prosta y=2 też jest funkcją liniową
więc
m2 − 6 > 0
Jak rozwiązać takie coś mam nadzieję, że wiesz
 3)
y=a(x−2)2+5
y(1)=8
8=a(1−2)2+5
3=a
3)
y=a(x−2)2+5
y(1)=8
8=a(1−2)2+5
3=a
 Przepraszam bardzo, funkcja ma być rosnąca... więc zero nie może być...
czyli wlasciwie tak jak napisalem
m2 − 6 > 0
(m−√6)(m+√6) > 0
m ∊ ( − ∞; √6) U (√6 ; ∞)
Przepraszam bardzo, funkcja ma być rosnąca... więc zero nie może być...
czyli wlasciwie tak jak napisalem
m2 − 6 > 0
(m−√6)(m+√6) > 0
m ∊ ( − ∞; √6) U (√6 ; ∞)
| −b | −3 | 3 | ||||
Iksowa wierzchołka (P) = | = | = | ||||
| 2a | −2 | 2 |
| 3 | ||
skoro wierzcholek lezy w przedziale <1;4> (bo wynosi | ) | |
| 2 |
| 3 | 25 | 1 | ||||
f( | ) = | = 6 | ||||
| 2 | 4 | 4 |
| 3 | 25 | 1 | ||||
f( | ) = | = 6 | ||||
| 2 | 4 | 4 |
| 3 | 1 | |||
Widzimy wartość maxymalną w wierzchołku ... f( | ) wynosi 6 | |||
| 2 | 4 |
 To teraz ja zabieram się za analize
To teraz ja zabieram się za analize  Dziękuje raz jeszcze !
Dziękuje raz jeszcze !