Nierówności wymierne
lanafane: Rozwiąż nierówność
x−4/5−x − 1/1−x ≤ 0
17 gru 19:17
Jack: mógłbyś zapisać za pomocą U te ułamki? lepiej by było widać.
| x−4 | | 1 | |
| − |
| ≤ 0 <−−−tak to ma wyglądać? |
| 5−x | | 1−x | |
17 gru 19:19
Jack: wspólny mianownik i wio : D
17 gru 19:21
lanafane: tak tak
17 gru 19:21
lanafane: Sprowadziłam do wspólnego i coś nie wyszło....
17 gru 19:22
Jack: co oznacza coś nie wyszło ? : D
w liczniku masz : x2 −4x − 1
mianownik : (5−x)(1−x)
Liczysz delte z licznika...
17 gru 19:26
lanafane: Mi w liczniku wyszło −x2 +4x ....
17 gru 19:28
lanafane: O jaaa...Dobra widze swój błąd
17 gru 19:28
lanafane: Dzięki

17 gru 19:28
Jack: To wymnóż jeszcze raz...
| (x−4)(1−x) − 1(5−x) | |
| |
| (1−x)(5−x) | |
17 gru 19:29
lanafane: Ale jednak wychodzi −x2+6x−9
17 gru 19:30
Jack: Z tego co widzę, to mi wyszło :
x ∊ <2−√5 ; 1) U (5; 2+√5>
17 gru 19:30
Jack: oj faktycznie, jak najbvardziej masz rację
17 gru 19:32
Jack: Raczej widzisz że to jest wzór skróconego mnożenia...
czyli wynik
x∊(−∞;1) U (5;∞)
17 gru 19:33
lanafane: a skąd te pierwiastki ? (x−4)(1−x)−1(5−x) = x − x2 −4 + 4x −5 +x = −x2+6x−9
17 gru 19:34
Jack: zły nawias zrobiłem...post 19:30 jest zły, natomiast poprawny jest 19:33
17 gru 19:35
lanafane: Jeszcze {3}
17 gru 19:39
lanafane: Z tym że metodą wężykową mi nie wychodzi...
17 gru 19:39
lanafane: ale tabelą znaków wyszło, dobra
17 gru 19:41
Jack: Jak to nie wychodzi
i dlaczego 3?
17 gru 19:41
lanafane: Bo 3 jest rozwiązaniem równania −x2+6x−9
17 gru 19:42
lanafane: Swoją drogą wężykową jednak wyszło
17 gru 19:44
Jack:
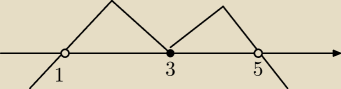
otrzymujesz
≤0 jest dla x∊(−
∞;1) U (5;
∞) U {3}
Czyli tak, z trójką miałeś rację.
17 gru 19:46
Metis: A co z dziedziną?
17 gru 20:00
lanafane: No dziedzina R − {1,5} , zatem przedział otwarty
17 gru 20:02

 otrzymujesz
otrzymujesz