Oblicz pole powierzchni figury ograniczonej krzywymi kamilah102: Oblicz pole powierzchni figury ograniczonej krzywymi: a) y=x² − 3x i y=x+5 b) y=x − 2x i y= −x²+3x+3 c) y=x² − 2x−3 i y=5 d) y=x² − 2x−3 i y=−2x+1

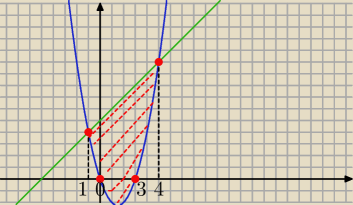
Eta: I teraz poproś całkę oznaczoną ..............

kamilah102: szczerze mowiac to sa moje zadania na kolokwium a nic z tego nie rozumiem, prosze o pomoc

kamilah102: szczerze mowiac to sa moje zadania na kolokwium a nic z tego nie rozumiem, prosze o pomoc

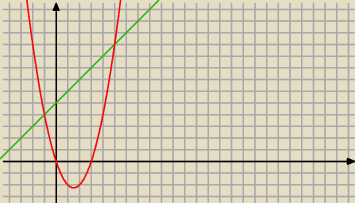
bezendu: a) f(x)=x²−3x g(x)=x+5 całka w granicach x∊[−1,5] ∫[x+5−(x²−3x)]dx=∫(x+5−x²+3x)dx

	1
∫(−x2+4x+5)dx=−∫x2dx+4∫xdx+5∫dx=−		x3+2x2+5x+C
	3

Wstawiam granice całkowania:

	1		100		8		108
[−		x3+2x2+5x]|=		+		=
	3		3		3		3

=================================

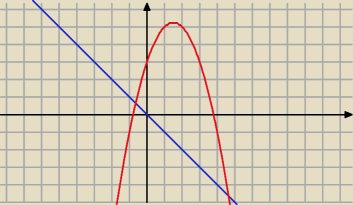
bezendu: b) f(x)=x−2x g(x)=−x²+3x+3 całka w granicach x∊[2+√7 , 2−√7] ∫[−x²+3x+3−(x−2x)]dx=∫(−x²+3x+3−x+2x)dx

	1
=∫(−x2+4x+3)dx=−∫x2dx+4∫xdx+3∫dx=−		x3+2x2+3x+C
	3

Wstawiam granice całkowania:

	1		34+14√7		34−14√7		28√7
[−		x3+2x2+3x]|=		−(		)=
	3		3		3		3

=================================

bezendu: b) mała pomyłka granice całkowania x∊[2−√7, 2+√7]

Eta:

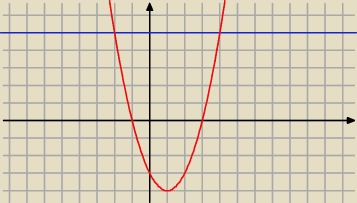
bezendu: c) g(x)=x²−2x−3 f(x)=5 Całka w graniach x∊[4,−2] ∫[5−(x²−2x−3)]dx=∫(5−x²+2x+3)dx=∫(−x²+2x+8)dx

	1
=−∫x2dx+2∫xdx+8∫dx=−		x3+x2+8x+C
	3

Wstawiam granice całkowania:

	1		80		28		108
[−		x3+x2+8x]|=		+		=
	3		3		3		3

=================================

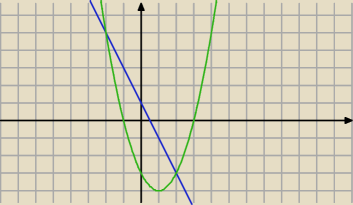
bezendu: d) g(x)=x²−2x−3 f(x)=−2x+1 Całka w granicach x∊[2,−2] ∫[−2x+1−(x²−2x−3)]dx=∫(−2x+1−x²+2x+3)dx

	1
=∫(−x2+4)dx=−∫x2dx+4∫dx=−		x3+4x+C
	3

Wstawiam granice całkowania

	1		16		16		32
[−		x3+4x]|=		+		=
	3		3		3		3

=================================