ekstrema funkcji uczen: Wyznacz ekstrema funkcji (o ile istnieją) fukcji f: f(x)= x³+8x²+21x+18 dla x<−2

	x2−4
f(x)=		dla x≥−2
	x2+1

Obliczyłem f'(x)= 3(x+3)(x+2¹₃) dla x<−2

	10x
f'(x)=		dla x≥−2
	(x2+1)2

Z tego ekstrema M=0 w x=−3 m=⁻⁴₂₇ w x=−2¹₃ m=−4 w x=0 Nie wiem jednak jak dojść do wniosku, że M jest również w x=−2 − widzę, że pochodna najpierw rośnie od −2¹₃ a potem maleje do 0, ale przecież nie jest równa 0 w x=−2, dlaczego więc w tym punkcie funkcja ma ekstremum?

uczen: Czy jest ktoś kto mógłby pomóc?

cosinusx: W x=−2 funkcja nie przyjmuje ekstremum, gdyż nie jest spełniony warunek konieczny, czyli f'(−2)≠0. Piszesz: "widzę, że pochodna najpierw rośnie od −213 a potem maleje do 0" −ale przecież to nie jest ta sama pochodna, bo na tych przedziałach funkcja jest określona innymi wzorami. W punkcie x=−2 funkcja jest nieciągła. Z definicji ekstremum: funkcja przyjmuje w x=−2 ekstremum maksimum (minimum) jeśli w otoczeniu tego punktu wartości funkcji są mniejsze (większe). 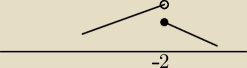Spójrz na rysunek− dla x=−2 funkcja przyjmuje większe wartości dla x<−2, więc to nie może być ekstremum. Mam nadzieję, że pomogłam.

uczen: Bardzo dziękuję, już rozumiem