Planimetria Równoległobok : równoległobok a'b'c'd' jest obrazem równoległoboku abcd w symetrii względem punktu 0,0. Oblicz pole wspólnej części tych równoległoboków. A(−4,−2) B(4,−2) C(7,3) D(−1,3) Proszę o pomoc

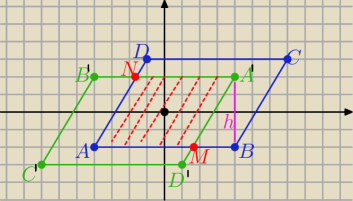
Eta: Punkt P(x,y) symetryczny względem S(0,0) to P^'(−x,−y) zatem A^'( 4,2), B^'(−4,2), C^'(−7,−3) , D^'(1,−3) wysokość równoległoboku AMA^'N jest równa |A^'B|= √(4−4)²+(−2−2)²= 4 P(AMA^'N)= |AM|*h M(x,y) jest punktem wspólnym prostych AB i A^'D

	−3−2
AB: y=−2 i A'D : y=		(x−4)+2 ⇒ A'D : 5x−3y−14=0
	1−4

	8		8
zatem : 5x−3(−2)−14=0 ⇒ x=		M(		, −2)
	5		5

	8		28
|AM|= 4+		=		= 5,6
	5		5

P(AMA^'N)= 5,6*4= 22,4 [j²]

Równoległobok : Dziękuję

Eta:

MARTA: MAM PYTANIE OBLICZAJĄC ODCINEK |AM| =4+8/5 ..............SKĄD TE 4 ?

6latek: Wydaje sie ze odleglosc punktu A od osi OY wynosi 4 (odczytane z rysunku )

chichi: Jak nie widzisz z rysunku, to licz ze wzoru na odległość punktu od prostej

MARTA: ALE JAK PODSTAWIAM DO WZORU NA ODLEGŁOŚĆ TO WYCHODZI CAŁKIEM INNY WYNIK

MARTA: SAM SPRÓBUJ TO ZOBACZYSZ

6latek: Wylacz te duze litery. Nie musisz krzyczec

chichi: A=(−4, −2), równanie prostej zawierającą oś OY: x=0 ! ! ! ! Ty zapewne liczysz odległość od prostej o równaniu y=0 A=1, B=0, C=0 ∧ x₀=−4, y₀=−2

	|Ax0+By0+C|		|1*(−4)+0*(−2)+0|		4
d=		=		=		=4
	√A2+B2		√12+02		1

Spróbowałem, zobaczyłem

6latek: |AB|= √8²+0²= √64=8 srodek odcinka AB x_s=0

	−4
ys=		=−2
	2

S=(0,−2) czyli lezy na osi OY wobec tego os OY jest symetralna |AB| a stad juz wiadomo dlaczego odleglosc punktu A do osi OY=4

Eta: