Sinus i cosinus kata astrolog: Dany jest kwadrat ABCD o boku 1. Niech punkt M nalezy do AB a punkt N do AC, AM=a, N jest rozny od C. Oblicz sinus i cosinus kata MCN.

grace: fajny temat

Astrolog:

Astrolog:

Astrolog:

Astrolog:

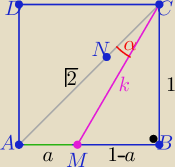
Eta: |AC|=√2 , |MB|=1−a , a∊(0,1) 1/ Z tw. Pitagorasa w ΔBMC: k²= 1+(1−a)² = a²−2a+2 z tw. cosinusów w trójkącie AMC:

	(√2)2+k2−a2		2−a
cosα=		= ..........=
	2√2*k		√2*√a2−2a+2

sinα= + √1−cos²α=...........

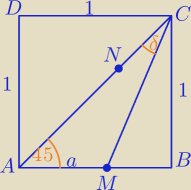Mila: 0<a<1 |AC|=√2 |MB|=1−a |CM|²=1²+(1−a)² |CM|²=1+1−2a+a²=2−2a+a²⇔ |CM|=√a²−2a+a

	1		√2		√2		a
PΔMAC=		*√2*a*sin(45o)=		*a*		=
	2		2		2		2

	1		1
PΔMAC=		*|AC|*|CM|*sinδ=		*√2*√a2−2a+a*sinδ⇔
	2		2

	√2*(a2−2a+2)
PΔMAC=		*sinδ
	2

porównujemy pola:

√2*(a2−2a+2)		a
	*sinδ=		⇔
2		2

√2*(a²−2a+2)*sinδ=a

	a
sinδ=
	√2*(a2−2a+2)

============== cosδ licz z jedynki tryg.

	√(a−2)2		|a−2|
cosδ=		=
	√2*(a2−2a+2)		√2*(a2−2a+2)

	2−a
cosδ=
	√2*(a2−2a+2)

==================

Eta: