Zadania optymalizacyjne analiza mat
Kacperix : Wyznacz dwie nieujemne liczby x i y, które spełniają równanie 2x+y=1 tak aby suma ich
sześcianów x3+y3 była największa. Doszedłem do tego ze musze obliczyć argument dla którego
pochodna w przedziale <0,,1/2> przyjmuje maksimum lokalne i wg mnie jest to X równe
| | 4−√2 | |
|
| ale w odpowiedziach podają ze X równą się 0 a y = 1 bardzo proszę o pomoc w |
| | 7 | |
rozwiązaniu tego jakże nurtującego mnie problemu
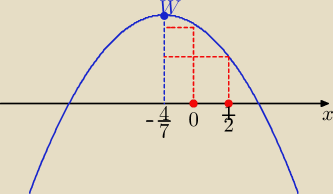 f'(x) >0 ⇔ −7x2−8x+2>0 i x∊<0,1/2>
ymax= f(0) = 2*0+1= 1 dla x=0
f'(x) >0 ⇔ −7x2−8x+2>0 i x∊<0,1/2>
ymax= f(0) = 2*0+1= 1 dla x=0