Nierówności trygonometryczne Piotr: 1. tgx−ctgx>0 2. sinx(cosx−0.5)>0, gdzie x należy <0, 2π>

Jerzy:

	1
1) tgx = t ..... ⇔ t −		> 0
	t

Jerzy: 2) ⇔ sinx > 0 i cosx − 0.5 > 0 lub sinx < 0 i cosx − 0.5 < 0

Piotr: Czy w pierwszym mogę pomnożyć przez t? Żeby zostało t²−1>0 ? W drugim wyszło x należy (0, π/3) ∪ (π, (5π/3)). Nadal nie wiem dlaczego trzeba sprawdzić drugi przypadek czyli że sin<0 i cos−0.5<0.

Jerzy: 1) ⇔ (t² −1)*t > 0 2) a*b > 0 ⇔ a > 0 i b > 0 lub a < 0 i b < 0

ICSP: W pierwszym można również skorzystac z tożsamości : tgx − ctgx = −2ctg(2x)

Piotr: W drugim już mam dobrze. W pierwszym mam zrobić podobnie jak w drugim? Czyli że: tg²−1>0 ∧ tg>0 lub tg²−1<0 ∧tg<0 ? Bo jeśli tak robię to wychodzi mi tylko połowa odpowiedzi dobrze. Z pierwszego jest x⬡należy (π/4+kπ, π/2+kπ) i jeszcze powinna być ∪ (3π/4+kπ, π+kπ)

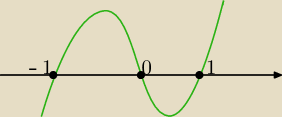
Jerzy: f(t) = t*(t² − 1)