Pomocy Krzyś : Prosta l przechodzi przez punkt D=(−3;2) i przecina osie układu współrzędnych w takich punktach A i B że |AB|=4√5. Napisz równanie tej prostej l, gdy współczynnik kierunkowy jest liczbą całkowita. Mógłby mi to ktoś wyjaśnić?

Eta:

	−b
A(		,0) , B(0,b) i a∊C \{0} |AB|=4√5
	a

AB: y=ax+b i D(−3,2) ∊AB to 2=−3a+b ⇒ b= 3a+2

	−b		−3a−2		−2
to		=		= −3+		a jest dzielnikiem 2
	a		a		a

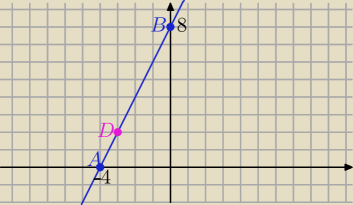
a=±1 lub a=±2 sprawdzamy dla : a=1 ... a= −1 ... a= −2 tylko dla a=2 spełnione są warunki zadania wtedy b=8 to A(−4,0) , B(0,8) |AB|=√16+64=√80=4√5 ...ok AB: y= 2x+8