Ściana boczna ostrosłupa prawidłowego sześciokątnego jest nachylona do podstawy pod kątem 30o,
a wysokość tej ściany jest równa 3√3. Oblicz objętość tego ostrosłupa.
x=H
| √3 | ||
y= | (wysokość ściany bocznej) | |
| 3 |
| a√3 | ||
z= | (wysokość trójkąta równobocznego o krawędzi a) | |
| 2 |
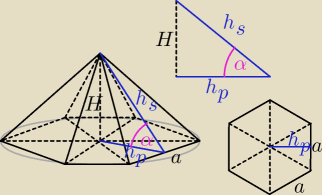hs = 3√3
α = 30o
| H | 1 | ||
= sin30o = | |||
| hs | 2 |
| 3 | ||
H = | √3 | |
| 2 |
| hp | √3 | ||
= cos30o = | |||
| hs | 2 |
| 9 | ||
hp = | ||
| 2 |
| 2 | ||
a = | √3hp = 3√3 | |
| 3 |
| a2√3 | ||
V = | *H = | |
| 2 |