ciągi mateusz: ciągi studia jak radzić sobie z takimi zadaniami, poproszę o pomoc 1) zbadaj ograniczoność ciągu a_n = n⁽⁻¹⁾ⁿ

	(−1)n		(2n + 1)!
2) badać zbieżność ciągu an =		*
	n		(2n)!

sushi_gg6387228: a) policzyc na piechote kilka poczatkowych wyrazów ciagu b) rozpisac silnie

Janek191:

	( −1)n * (2 n + 1)		1
2) an =		= (−1)n*( 2 +		)
	n		n

mateusz: Janku z czego się zrobiło to przekształcenie bez mianownika już ?

mateusz: sushi_gg6387228 ale jak tak na piechotę i tyle ?

zeesp: jak doliczysz do nieskończoności to daj znać

Janek191: Wykonano dzielenie przez n.

mateusz: zeesp <biorę się do roboty > a tak na poważnie, to jak z tym działać

sushi_gg6387228: piechota == pokazuje pomysł w głowie do czego to dąży−−> potem można brać się za pokazywanie ograniczenia/braku

zeesp: chodzi o to, żebys zauważyl co tam sie dzieje..a potem wyciągnął ogólny wniosek.

mateusz: Janek191

	(−1)n
gubię się przy tym		to ile?
	n

mateusz: a) wyraz pierwszy to 1 pozostałe skaczą w stronę nieskończoności i jedyni, na przemian

sushi_gg6387228: podstawiaj na piechote i wyciagnij wniosek

sushi_gg6387228: a) wypisz je a₁=.. a₂=.. a₃=...

Janek191: 1) a _n = n⁽⁻¹⁾ⁿ ?

mateusz:

	1		1
1,2,		,4,		..
	3		5

sushi_gg6387228:

	1
i		dązy wg Ciebie do ∞?
	5

mateusz: Janek191 tak

mateusz: tak jak napisałem na przemian dążą do nieskończoności i jedynki,/ ułamki do jedynki

Mila:

	1
Rysujesz wykres y=
	n

	1
an=		→0 dla n→∞
	n

	−1
a1=		=−1
	1

	(−1)2		1
a2=		=
	2		2

	−1)3		1
a3=		=−
	3		3

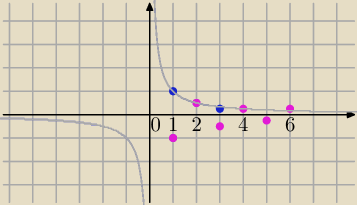
różowe na wykresie.

	1
Ograniczony z góry przez		z dołu przez (−1)
	2

sushi_gg6387228: źle bo rozsądna osoba by napisała n⁻ⁿ a nie n⁽⁻¹⁾ⁿ tam masz w wykładniku potegi (−1)ⁿ

mateusz: skąd wykres się wziął

mateusz: przepisuje tak jak mam podane n⁽⁻¹⁾ i minus jeden do potęgi n

mateusz: wzór taki jak 17;17 u Janka

Mila: Ja rozważyłam ciąg

	(−1)n
an=
	n

sushi_gg6387228: post 17;19 liczby podane nie do tego przykładu

Mila: To już Was zostawiam, bo tu za dużo osób.

mateusz: zamieszałem w końcu sam

mateusz: badając zbierzność musze określić czy ma granice lim w nieskończoności, jeśli ma to jest zbieżny tak ?

Mila: Zbieżność czego?

mateusz: ciągu

mateusz: np przykład 2) chodzi o to jak rozwiązywać

Mila: Jane rozpisał.

	1
an=(−1)n*(2+		)
	n

	1
limn→∞(2+		)=2
	n

(−1)ⁿ ciąg naprzemienny nie istnieje granica. Natomiast :

	1		1
lim n→∞(−1)n*		=0 bo (−1)n to ciąg ograniczony ,a ciąg		→0
	n		n

mateusz: nadal nie rozumiem zapisu, skoro się dzieli przez n tak jak napisał Janek to co 17:41

Mila: Jakiego zapisu, napisz precyzyjnie o co Ci chodzi.

mateusz: 17;03 Janka nie wiem jak potem zniknęło to n z mianownika niby przez dzielenie ale nie rozumiem jak podzielił i zapytałem 17:41

mateusz: ahahhhh 17:14

Mila:

	(−1)n
limn→∞		=0
	n

bo możesz to zapisać jak napisałam 20:23 po słowie natomiast.

mateusz: dobrze kapuje dziękuję