Równanie ma dwa różne pierwiastki Jacek:

	x2 + a
Równanie		= 8 ma dwa różne pierwiastki dla dowolnej liczby a ze zbioru. Wiem,
	x

że powinno wyjść (−∞;0)∪(0;16). Mi wychodzi (−∞;16). Wiem, że x≠0 i, że prawidłowy wynik wynika właśnie z tej dziedziny ale nie rozumiem dlaczego mam uwzględniać tutaj dziedzinę x skoro obliczam zbiór dla a. Proszę o wytłumaczenie.

Krzysiek : x jest niewiadona i a to parametr

henrys:

	x2
dla a=0 dostajesz równanie		=8, które ma 1 rozwiązanie
	x

henrys: Zauważ, że sprowadzając podane równanie do równania kwadratowego x²−8x+a=0 otrzymujesz dwa rozwiązania dla a<16, jednak x=0 nie należy do dziedziny tego równania. Tak więc w punkcie x=0 parametr a przyjmowałby wartość zero i właśnie ze względu na dziedzinę musimy a=0 wykluczyć z szukanego zbioru.

Jacek: Ok rozumiem. Ale niestety gdybym nie znał odpowiedzi byłbym pewien, że (−∞;16) to poprawny wynik. Dzięki za odpowiedzi

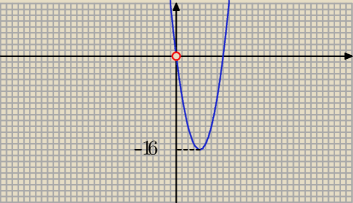
henrys: Zadanie możesz rozwiązać również tak: x(x−8)=−a, x≠0 wtedy dla −a>−16 i a≠0 równanie będzie miało dwa rozwiązania czyli dla a∊(−∞,0)∪(0,16)