sprawdzenie szereg mateusz: do sprawdzenia, jesli ktoś może proszę i dziękuję kolokwium w środę a ja z materiałem po technikum mogę sobie płakać bo tyle zaległości po starej podstawie mam .... jeszcze na studiach denerwującą rzeczą jest podawanie przez wykładowców zadań bez odpowiedzi rozwiąż

	1		1		1		2
1 +		+		+		+ ... =
	2cosx		4cosx		8cosx		2cosx

liczę

	1
q =
	2cosx

	a1
S =		więc
	1 − q

2		2cos
	=		podstawiam sobie t
2cosx		2cosx − 1

	π
i wychodzi t =0 więc x =		+ kπ
	2

Qulka: założenie |q|<1

Qulka: t≠0 bo mianownik

Qulka: jeżeli byłoby takie q jak podałeś przy cos rosłyby potęgi

J:

	1		1
błądzicie L = 1 + Sn i a1 =		i q =
	cos2x		2

Qulka: dziwne że po prawej masz 2 w liczniku i mianowniku.... czyżbyś chciał napisać całkiem coś innego?

J:

	1
a1 =
	2cosx

Qulka: i wtedy 1=0

mateusz:

	1
J : jak q wyliczyłeś tak że wyszło samo		?
	2

Mila: Prawą stronę masz dobrze zapisaną, przecie 2 upraszcza się.

mateusz: a już kapuje obrałeś dalej początek i tak wyliczyło się czyli gdy to zrobiłeś to tego nie trzeba rozpisywać że |q| < 1 ? bo to jest spełnione

mateusz: PRAWA STRONA ŻLE Przepraszam Was w komputerze źle i na kartkach źle liczone cały czas ...

	2
P =
	cosx

Mila: Liczyć?

Qulka: to cosx=1 więc x=2kπ

mateusz: doliczyłem to teraz tylko dla pewności tam wracam z szykiem że a₁ = 1 a nie tak jak przyjęło się/ do policzenia q że a₁ to U{1}[2cosx} chodzi to dla wzoru S = U{a₁}[1 − q}

mateusz: taki schemat jest na 100% w porządku do rozwiązywania zadań tego zarysu ? ten przykład jest dobrze rozwiązany tak ?

Mila: a₁=1

	1		π
q=		, cosx≠0⇔x≠		+kπ
	2cosx		2

|q|<1⇔

	1
−1<		<1
	2cosx

1		1
	>−1 i		<1
2cosx		2cosx

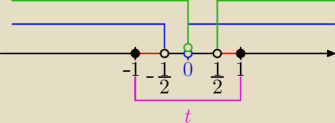
cosx=t, |t|≤1

1		1
	>−1 i		<1
2t		2t

1		1
	+1>0 i		−1<0
2t		2t

1+2t		1−2t
	>0 i		<0
2t		2t

2t*(1+2t)>0 i 2t(1−2t)<0⇔

	1		1
t∊<−1,−		) lub t∊(		,1> trzeba rozwiązać
	2		2

	1		1
−1≤cosx<−		lub		<cosx≤1 to w nowym wpisie bo, z wykresem
	2		2

ale, to wystarczy

	1		2cosx		2cosx
S=		*		=
	1   1−   2cosx		2cosx		2cosx−1

2cosx		2
	=
2cosx−1		cosx

Wynik jak u Qulki

mateusz: Mila złota kobieta dziękuję ale nie rozumiem trzeciej linijki od góry

Qulka: mila..że też Ci się chciało

	1
gdyby q=		to by ten ciąg wyglądał tak:
	2cosx

	1		1		1		1
1 +		+		+		+		+...
	2cosx		4cos2x		8cos3x		16cos4x

mateusz: to zawsze musze rozpisywać ten warunek |q| < 1? moge zostawić to tak jak Ty to Milu zrobiłaś z parametrem t i nie liczyć wartości dla cos ?

Qulka: i dlatego mówiłam że nie należy tak liczyć jak liczył

Qulka: jeżeli chcesz użyć wzoru na zbieżny, to musi być zbieżny, czyli mieć |q|<1

mateusz: czyli gdy roziwiązuje na kolokwium takie zadania to w tym wszystkim musi się znaleźć to |q|<1

Mila: Powinno się rozwiązać, ale to ostatnie, gdzie już masz warunek na cosinusy możesz zostawić (?) z tym że trzeba rozwiązanie ostatniego równania sprawdzić z tym warunkiem. Jednak warunek musisz do tego miejsca doprowadzić..

Mila: Dobranoc , działajcie dalej.

mateusz: dobranoc dzieki za pomoc

Qulka: jeśli na końcu równania miałeś ... a chcesz wstawić sumę to musisz mieć |q|<1

mateusz: cały czas wnioskuje że mogę to zrobić inaczej bez tego z tych waszych wypowiedzi Qulka czyli że jak bez wzoru na sumę

Qulka: zależy od zadania tu u Ciebie ponieważ nie rosną potęgi więc trzeba tak jak J pisał zostawić 1 i zająć się resztą wtedy a₁ = 1/2cosx i q=1/2 i widać że |q|<1

	a1		2		1
i masz sumę z S =		=		=
	1−q		2cosx		cosx

wracamy do równania

	1		2
1+		=
	cosx		cosx

więc cosx=1

mateusz: sam już nie wiem szczerze jak z tym jest hahha zrobię następny przykład 2^3x + 2^{3x − 1} + 2^{3x − 2} + 2^{3x − 3} + .... = √12 * 2^3x − 8 liczę q

	23x − 1		1
q =		= 2−1 =
	23x		2

	a1
S =
	1 − q

√12 * 2^3x − 8 = 2^3x * 2 podstawiam żeby nie zgubić się t = 2^3x ale czy tak mogę √12 * t − 8 = t * 2 12t − 8 = 4t² delta t₁ = 1 t₂ = 2 wracam z t

	1
i wynik mam taki że x = 0 albo x =
	3

czy to ma sens?

Qulka: możesz podstawić t ale trzeba założyć że t>0 tak ma