Symetria osiowa
Nieumiejętny : Kwadrat K2 jest obrazem kwadratu K1 w symetrii względem osi OX, a kwadrat K3 jest obrazem
kwadratu K1 w symetrii względem osi OY. Oblicz pole części wspólnej kwadratów K1 i K2 oraz
pole częsci wspólnej Kwadratów K1 i K3. Wierzchołki kwadratu K1:(1, −2); B(5,2); C(1,7);
D(−3,2). I narysowałem, odbiłem, policzyłem długości odcinków, znaczy boków i te dla części
wspólnych, te krótsze boki itp. i wyszło mi, że Pole wspólne dla K1 i K2 to 2, a dla K1 i K3
to 5. I nie pasuje









Proszę o pomoc dobre Duszyczki



12 gru 21:56
Saizou :
kąt ADC nie jest prosty

12 gru 22:02
12 gru 22:18
Nieumiejętny : Możesz pokazać to tutaj, że nie


Bo rysowałem i mi wychodzi..
12 gru 22:19
Mila:
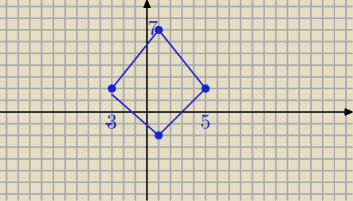
12 gru 22:29
5-latek :
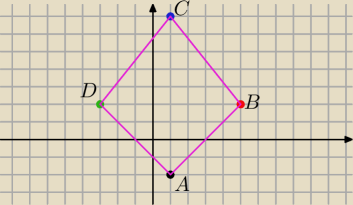
wektor DA= [4 −4]
wektor DC= [4,5]
Iloczyn skalarny DAoDC= [4 −4]o[4 5] = 4*4+(−4*5)= −4≠0
Wektory nie sa prostopadle zatem kat ADC nie jest prosty
12 gru 22:42
Nieumiejętny : Kurde..to nie wiem..:(:(:( Idzie tutaj jakoś dodawać pliki, zdjęcia? Bo bym wstawił zdjęcie
tego zadania...:(
12 gru 22:55
5-latek : Dane sa zle Zobacz na rysunku ze przekatna AC ma dlugosc 9 a przekatna BD ma dlugosc 8
A tak w kwadracie być nie może
12 gru 23:07
Mila:
Może C=(1,5)
12 gru 23:10
5-latek: Milu może bardziej C=(1,6)
12 gru 23:14
Nieumiejętny : TAK! Przepraszam, źle odczytałem z rysunku

12 gru 23:36
Nieumiejętny : C (1,6)
12 gru 23:37
Nieumiejętny : Pomógłby ktoś? Bo to jest akurat nie ważne, ta pomyłka. Bo tego punktu akurat na brałem do
obliczeń.

13 gru 14:00
Saizou :
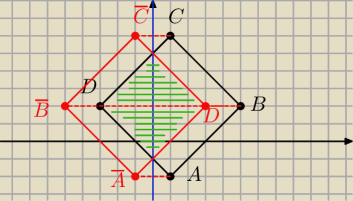
Względem osi OY
| | 1 | |
zatem Pz= |
| *6*6=18 [j2] |
| | 2 | |
analogicznie względem osi OX
13 gru 14:11
13 gru 14:20
Krzysiek : To np punkt A jakie ma wspolrzedne w odbiciu wzgledm osi OX ?
I tak pozostale punkty
13 gru 14:28
Nieumiejętny : Ahh....już wiem. Z punktami po odbiciu nie miałem problemu, tylko przy liczeniu, traktowałem to
jako kwadrat, liczyłem długości boków ze wzoru i dlatego mi coś nie wychodziło, bo wystarczy
policzyc ze wzoru na romb z przekątnymi. I stąd w tym pierwszym przykładzie 1/2*6*6 6 i6 to
przekątne


13 gru 14:37








 Proszę o pomoc dobre Duszyczki
Proszę o pomoc dobre Duszyczki 















 Bo rysowałem i mi wychodzi..
Bo rysowałem i mi wychodzi..

 wektor DA= [4 −4]
wektor DC= [4,5]
Iloczyn skalarny DAoDC= [4 −4]o[4 5] = 4*4+(−4*5)= −4≠0
Wektory nie sa prostopadle zatem kat ADC nie jest prosty
wektor DA= [4 −4]
wektor DC= [4,5]
Iloczyn skalarny DAoDC= [4 −4]o[4 5] = 4*4+(−4*5)= −4≠0
Wektory nie sa prostopadle zatem kat ADC nie jest prosty


 Względem osi OY
Względem osi OY




