dziedzina funkcji (trygonometria) mateusz: cześć mam takie zadanie zrobiłem ale nie do końca, i nie wiem czy dobrze poproszę o sprawdzenie f(x) = √cos²x + ¹₂cosx + (^2π₃ − |x − ^5π₃|) robie założenia 1⁰ {cos²x + ¹₂cosx ≥ 0 z czego wychodzi mi x ∊ <−^π₂ + 2kπ, ^π₂ + 2kπ> x ∊ <^2π₃ + 2kπ, ^4π₃ + 2kπ> 2^{0 2π}₃ − |x − ^5π₃| > 0 x ∊ <^3π₃, ^7π₃> ////////////////////////////////////// czy to jest ok ? jaką dać odp

ax: a co ma 2^o do dziedziny ?

mateusz: pomyłka tam log przedtem był

mateusz:

Mila: 1^o dobrze 2^o w drugiej nierówności

	7π
x∊(π,		)
	3

Trzeba wziąć część wspólną .

mateusz: jak do tej części wspólnej dojść myli mnie zapis 2kpi gdyby nie to jakoś by się próbowało zaznaczać na osi

mateusz:

mateusz:

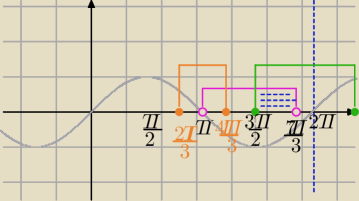
Mila: szkicujesz" lekko" wykres sin(x), aby mieć ustalone jednostki na osi.

	7π
x∊(π,		) to jest najmniejszy przedział,
	3

Dziedzina :

	π		π
x∊<−		+2kπ,		+2kπ>
	2		2

k=0

	π		π		7π
x∊<−		,		> ten przedział nie ma części wspólnej z przedziałem (π,		),
	2		2		3

k=1

	3		5π		7π
x∊<		π,		>∩(π,		) ⇔
	2		2		3

	3		7π
x∊<		π,		) jeden przedział.
	2		3

=============== Lub

	2		4
x∊<		π+ 2kπ,		π + 2kπ>
	3		3

k=0

	2		4		7π
x∊<		π,		π>∩(π,		)⇔
	3		3		3

	4π
x∊(π,		>
	3

========= Odp.

	2		4		4π
D=<		π+ 2kπ,		π + 2kπ>∪(π,		>
	3		3		3

============================

mateusz: muszę nad tym posiedzieć i samemu popróbować czy coś z tego mi wyjdzie mam podobne zadanie to podam potem do sprawdzenia dziękuję