równanie z parametrem Ilona: wyznacz wszystkie wartości parametru m dla których równanie |(x+3)² −1|=|m+2| Rozwiązujemy tego typu zadania za pomocą wykresu. Nie wiem jak doprowadzić by po jednej stronie była sama litera m bez wartości bezwzględnej, a po drugiej cała reszta równania. Prośba o rozpisanie tego początku, dalej sobie poradzę.

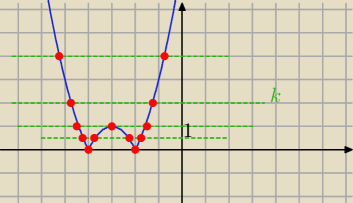
Eta: Zapisz prawą stronę : y=k= |m+2| dla k=0 lub k>1 dwa roazwiązania i rozwiąż teraz : |m+2|=0 lub |m+2|>1 ⇒ m∊ ................ dla k∊(0,1) −−− 4 rozaiązania zatem |m+2|>0 i |m+2|<1 ⇒ m.............. dla k=1 −− 3 rozwiązania zatem |m+2|=1 ⇒ m=.......... dla k<0 −−− brak rozwiązań zatem |m+2|<0 ⇒ m...............

ax: jak wszystko w matematyce można na różne sposoby np tak |a|=|b| to a=b lub a=−b Zatem: (x−3)²−1=m+2 lub (x−3)²−1=−m−2 (x−3)²−3=m (x−3)²+1=−m

Ilona: nie dokończyłam treści zadania w sumie wyznacz wszystkie wartości parametru m dla których równanie |(x+3)2 −1|=|m+2| ma dwa rozwiązania różnych znaków. Dzięki za podpowiedzi − już wiem jak zrobić