Kwadratowa. Ewka: Dla jakich wartości parametru m równanie: x²− (m+1)|x| +1 = 0 ma dwa różne rozwiązania? Rozpatrzyłam dla dwóch przypadków x≥0 i x<0. Wyszło mi że x∊(−∞, −3) ∪ (1, +∞). Czy tak to trzeba zrobić?

sushi_gg6387228: zapisz swoje obliczenia szukamy "m"

Ewka: No tak m∊(−∞, −3) ∪ (1, +∞) . No obliczenia raczej proste dla dwóch przypadków wyszło mi że m² + 2m −3 > 0 .

sushi_gg6387228: piszemy po kolei x≥ 0 ......

Ewka: No dobra to tak: x≥0, wtedy: x²−(m+1)x +1 =0 Δ= m² +2m +1 −4⇒ m² + 2m −3. Δ_m = 16 m₁ = 1 , m₂ = −3 No i teraz rysuje parabole i odczytuje dla większych od zera i wychodzi m∊(−∞, −3) U (1, ∞). Dla x<0 , wtedy: x²+(m+1)x +1 =0 Δ= m² +2m +1 −4⇒ m² + 2m −3. Δ_m = 16 m₁ = 1 , m₂ = −3 Czyli to samo czy to jest poprawnie?

sushi_gg6387228: x ≥ 0 Δ>0 dla m ∊ (−∞; −3) u (1; ∞) trzeba sprawdzić jakie będą x₁ i x₂

Ewka: Czyli mam wybrać jakiś m z tego przedziału i narysować tę funkcję w tych przedziałach tzn x≥0 i x<0 ?

sushi_gg6387228: nie trzeba sprawdzić na podanej Δ czy x₁ i x₂ beda dodatnie bo jakby wyszło jeden dodatni i jeden ujemny to lipa

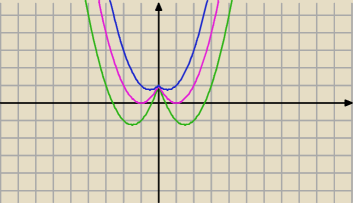
ax: może to Ci pomoże Bo sushi .... nie zawsze jest strawne

Ewka: Czyli w pierwszym przypadku x₁ i x₂ muszą być dodatnie a w drugim ujemne bo to wynika z założeń tak?

sushi_gg6387228: tak

Ewka: No to zrobiłam ze wzorów Vieta i wyszło mi w 1 przypadku że m∊(−1,∞) , a w drugim że m∊(−∞,−1) i co mam zrobić teraz część wspólną z założeniem Δ > 0?

sushi_gg6387228: Kto kazał liczyć Viete'a ?

Ewka: No skoro dwa miejsca zerowe mają być dodatnie to muszą spełniać x₁x₂ >0 i x₁ + x₂ >0 tak?

Ewka: Dobra, ugryzłam to z tej strony co zaproponował ax. Napisałam że funkcja x² −(m+1)|x| +1 = 0 będzie miała 2 różne rozwiązania wtedy kiedy funkcja f(x) = x² − (m+1)x +1 = 0 będzie miała 1 rozwiązanie dodatnie bo jak odbijemy f(|x|) to dostaniemy drugie miejsce zerowe. Czy to rozumowanie jest dobre?

ax: bingo