asymptoty Maciej: Zbadaj istnienie asymptot następujących funkcji:

	sinx
f(x) = x +
	x

Pionowej na pewno nie ma. Dalej mam problem... Nie wiem jak obliczyć te granice Proszę o pomoc. Odpowiedź to: asymptota pozioma y=1

	sinx
Jak policzyć granicę		gdy x dąży do NIESKONCZONOŚCI? Możemy policzyć w zerze lub w
	x

punkcie, ale w nieskonczoności chyba nie istnieje? Czy mój tok rozumowania jest zły?

Jerzy:

	f(x)
a = lim
	x

b = lim[f(x) − a*x] policz i dostaniesz asymptotę poziomą: y = 1

Maciej: znam te wzory, ale nie umiem policzyć granic niestety

Maciej : Potrafię liczyć granice, ale nie wiem jak mam tutaj poradzić sobie z tym sinusem... Wytłumaczyłby ktoś to łopatologicznie?

Janek191:

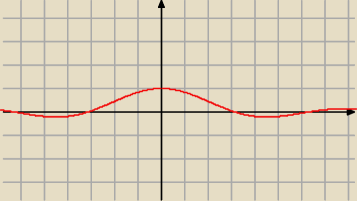
	sin x
lim		= 0, bo − 1 ≤ sin x ≤ 1
	x

x→∞

Maciej : Aaaa to w taki sposób należy patrzeć... Dziękuję bardzo, teraz rozumiem!

Janek191:

f(x)		sin x
	= 1 +
x		x2

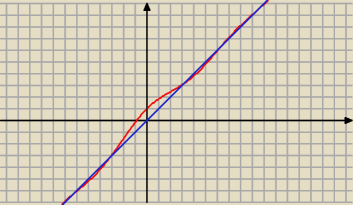
więc

	f(x)
lim		= 1 = a
	x

x→ ∞

	sin x
f(x) − 1*x =
	x

więc lim ( f(x) − x ) = 0 = b x→∞ y = a x + b = 1*x + 0 = x y = x − asymptota ukośna −−−−−−−−−

Maciej: czyli pozioma jest czy jej nie ma w końcu?

Janek191: Masz wykres − 16.34

Maciej: No okej, czyli odpowiedzi kłamią ale jeszcze raz bardzo dziękuję