Dwa okręgi o środkach
GkkG: Dwa okręgi o środkach S1 i S2 przecinają się w punktach A i B i leżą po przeciwnych stronach
prostej AB. Miary kątów wynoszą ∡AS1B=90 oraz ∡AS2B=60 wyznacz długości promieni tych
okręgów przy założeniu że |S1S2|=a.
12 gru 11:40
PW: Na pewno dobrze przepisana treść zadania?
Jakoś nie umiem sobie wyobrazić okręgów, które leżą po przeciwnych stronach prostej i
jednocześnie przecinają się w dwóch punktach.
12 gru 12:05
GkkG:
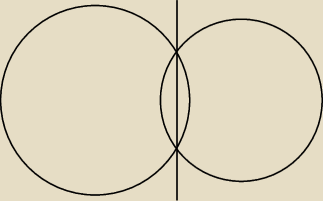
12 gru 12:35
PW: No i według Ciebie te okręgi leżą po przeciwnych stronach prostej?
12 gru 12:39
GkkG: W poleceniu chodzi o to że środki okręgów leżą po przeciwnych stronach prostej.
12 gru 12:54
PW: No to napisz dobrze polecenie, słowo w słowo, łącznie z interpunkcją.
12 gru 13:13
issk2: Przepisałem idealnie tak jak było w poleceniu. Mogę prosić o rozwiązanie?
12 gru 14:06
Eta:
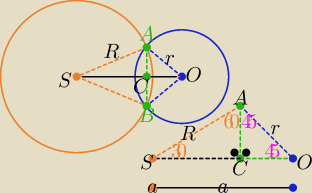
Z trójkątów ASC i ACO "ekierek"
| | r√2 | |
|AO|=r to |OC|=|AC|= |
| |
| | 2 | |
| | r√6 | |
zatem |SC|=r√3 = |
| to R=|AS|=r√2 |
| | 2 | |
| | r√6 | | r√2 | | a(√6−√2) | | a√2 | |
a=|SO|= |
| + |
| ⇒ ............ r= |
| = |
| (√3−1) |
| | 2 | | 2 | | 2 | | 2 | |
więc R= r
√2=............... = a(
√3−1)
12 gru 14:44
Eta:
W prowadziłam też inne oznaczenia S2=S i S1=O ( dla łatwości zapisów)
Zapomniałam zaznaczyć na rys. miar kątów
|∡AOB|=90o i |∡ASB|=60o
12 gru 14:49

 Z trójkątów ASC i ACO "ekierek"
Z trójkątów ASC i ACO "ekierek"