Optymalizacja
dawek:
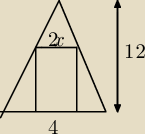
(trójkąt równoranienny)
Przedstaw pole P prostokąta jako funkcję zmiennej x. Prosiłbym z wytłumaczeniem

11 gru 19:26
===:
jeśli wysokość prostokąta zaznaczysz jako y
| 4 | | 2x | |
| = |
| ⇒ 48−4y=24x ⇒ 12−6x=y |
| 12 | | 12−y | |
P=2x(12−6x)
P=−12x
2+24x
11 gru 19:34
dawek: a jak wytłumaczyć ten stosunek?
11 gru 19:36
dawek: z kąd to 4/12=2x/12−y?
11 gru 19:40
===:
znasz niejakiego Talesa

a jak nie to z podobieństwa trójkątów
11 gru 19:50
Mila:
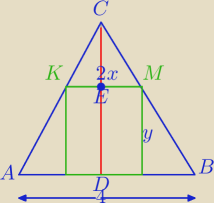
|KM|=2x
|AB|=4
h=|CD|=12
|CE=12−y
ΔKMC∼ΔABC⇔
| 2x | | 4 | | 2x | | 1 | |
| = |
| ⇔ |
| = |
| ⇔ |
| 12−y | | 12 | | 12−y | | 3 | |
6x=12−y
y=12−6x
P(x)=2x*(12−6x)
P(x)=−12x
2+24x , x<2
Największe pole prostokąta dla x=1
P(1)=2*(12−6)=12
11 gru 22:38
 (trójkąt równoranienny)
Przedstaw pole P prostokąta jako funkcję zmiennej x. Prosiłbym z wytłumaczeniem
(trójkąt równoranienny)
Przedstaw pole P prostokąta jako funkcję zmiennej x. Prosiłbym z wytłumaczeniem 
 a jak nie to z podobieństwa trójkątów
a jak nie to z podobieństwa trójkątów
 |KM|=2x
|AB|=4
h=|CD|=12
|CE=12−y
ΔKMC∼ΔABC⇔
|KM|=2x
|AB|=4
h=|CD|=12
|CE=12−y
ΔKMC∼ΔABC⇔