Znajdź brakujące współczynniki wielomianu
lepus: Znajdź brakujące współczynniki wielomianu w(x)=ax3+6x2+(6a2−4)x−48, jeśli wiesz, że
nierówność w(x)<0 jest spełniona (między innymi) przez wszystkie liczby rzeczywiste z
przedziału (−3;2).
10 gru 23:43
mati:
mój pomysł?
kiedy?
w(−3) ≥ 0
w(−2) ≥ 0
wziąć przekrój wyników, dla których a [ rozwiązać dwa równania 2 stopnia]
tak mi się wydaje, jak się mylę poprawcie mnie.
11 gru 00:31
Eta:
x
1= −3 , x
2=2 , x
3=k −− trzeci pierwiastek
W(x)=ax
3+bx
2+cx+d
ze wzorów Viete
'a
| | b | | d | |
x1+x2+x3= − |
| i x1*x2*x3= − |
| |
| | a | | a | |
| | −6 | | 48 | |
to k−1= |
| /*(−8 ) 8−8k= |
| |
| | a | | a | |
| | 48 | |
i −6k= |
| to: 8−8k= −6k ⇒ k= 4 to a= −2 |
| | a | |
(6a
2−4) = 20
W(x)=
−2x
3+6x
2+20x−48
11 gru 00:33
mati: | | 1 | |
a∊[−2, |
| ] oczywiście z brzegiem bo nierówność badaliśmy słabą a nie ostrą... |
| | 2 | |
11 gru 00:34
Eta:
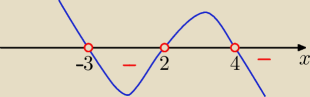 2 sposób
2 sposób
W(x)= a(x+3)(x−2)(x−k) = a(x
3−kx
2+x
2−kx−6x+6k)= ax
3+a(1−k)x
2+a(−k−6)x +6ak
to:
6ak= −48 ⇒ ak= −8
i a(1−k)=6 ⇒ a−ak=6 ⇒ a+8=6 ⇒ a= −2 to k= 4
itd.............
W(x)= −2x
3+6x
2+20x−48 i trzecim pierwiastkiem jest k= 4
11 gru 00:44
 2 sposób
W(x)= a(x+3)(x−2)(x−k) = a(x3−kx2+x2−kx−6x+6k)= ax3+a(1−k)x2+a(−k−6)x +6ak
to:
6ak= −48 ⇒ ak= −8
i a(1−k)=6 ⇒ a−ak=6 ⇒ a+8=6 ⇒ a= −2 to k= 4
itd.............
W(x)= −2x3+6x2+20x−48 i trzecim pierwiastkiem jest k= 4
2 sposób
W(x)= a(x+3)(x−2)(x−k) = a(x3−kx2+x2−kx−6x+6k)= ax3+a(1−k)x2+a(−k−6)x +6ak
to:
6ak= −48 ⇒ ak= −8
i a(1−k)=6 ⇒ a−ak=6 ⇒ a+8=6 ⇒ a= −2 to k= 4
itd.............
W(x)= −2x3+6x2+20x−48 i trzecim pierwiastkiem jest k= 4