Trygonometria Jasiu: Wyznacz wszystkie wartości parametru α∊<0,2π> , dla których równanie (x²−sinxα)(x−1)=0 ma trzy rozwiązania. Pomoże ktoś, jak mam się do tego zabrać?

===: (x−1)(x−√sinα)(x+√sinα)=0 i wszystko jasne

Jasiu: tyle, że to nie jest (x²−sin²x) tylko (x²−sinx) nie przeczytałeś dokładnie..

===: dobre sobie a pierwiastki widzisz

Jasiu: aa... sorry

Jasiu: chodzi mi raczej o to w tym zadaniu jak podstawić α do tych równań bo będę miał x=√sinα ⋁ x=√−sinα i x=1

Jasiu: Mam po podstawiać po prostu?

Jasiu: bo rozumiem, że α∊C

===: znaczy że nic nie rozumiesz

===: ...rozpisałeś ... tyle że ten minus to przed a nie pod pierwiastkiem A teraz odpowiedz dla jakich wartości kąta α te wyrażenia mają sens

Jasiu: źlę się wyraziłem chodzi mi o to że z przedziału <0,2π> całkowite tzn. 0,π,2π

===: źle

Jasiu: nie zbyt rozumiem mam podstawić liczby z przedziału <0,2π> jako alfę, x przy tym nie zmieniając?

Jasiu: x=√sinπ skąd mam wiedzieć czy to akurat pasuje..

Mila: (x²−sinα)(x−1)=0⇔ x²=sinα lub x−1=0 Równanie x²=sinα ma dwa rozwiązania dla sinα>0 i α∊<0,2π>⇔ α∊(0,π) [x=√sinα lub x=−√sinα i α∊(0,π)] lub x=1

Jasiu: czemu napisałaś przedział tylko dla sinα>0 ?

Jasiu: a co z sinα<0?

===: a jaka jest dziedzina f(x)=√x ?

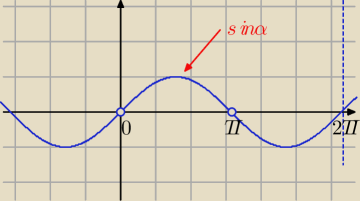
Mila: Bo pierwiastek kwadratowy wyciągamy z liczb≥0. x²=0 nie pasuje bo x=0 i to jest jedno rozwiązanie. więc sinα musi być dodatnie, a jest , jak wskazuje rysunek dla α∊(0,π)

Jasiu: A no tak , dzięki wszystkim

===: ... to jak to jest Mileńko ... ZERO wykluczasz ... a α=π/2

Mila: Racja sinα=1 x²=1⇔ x=1 ( a to już było!) lub x=−1 Zatem:

	π
α∊(0,π)\{		}
	2

===:

Mila: A Jasiu już nie patrzy .

===: Jasiu już pracę domową "odrobił"