zadanie optymalizacyjne marek: W jakim punkcie wykresu funkcji y = e^−x + 2 należy poprowadzić styczną, aby trapez ograniczony tą styczną i prostymi x = 1, x = 2, y = 0 (y ≥ 0) miał największe pole?

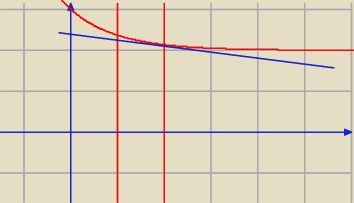
Godzio: Styczna w punkcie (x₀, e^−x₀+2) f(x) = e^−x + 2 f'(x) = − e^−x f'(x₀) = − e^−x₀ Równanie stycznej: y = − e^−x₀(x − x₀) + e^−x₀+2 Punkty przecięcia z prostymi x = 1 i x = 2: y(1) = − e^−x₀(1 − x₀) + e^−x₀+2 = x₀e^−x₀ + 2 y(2) = − e^−x₀(2 − x₀) + e^−x₀+2 = − e^−x₀ + x₀e^−x₀ + 2 Pole trapezu:

	x0e−x0 + 2 − e−x0 + x0e−x0 + 2
P(x0) =		* 1 =
	2

	2x0e−x0 + 4 − e−x0		e−x0
=		= x0e−x0 + 2 −
	2		2

Szukamy maksimum:

	e−x0
P'(x0) = e−x0 − x0e−x0 +		= 0
	2

	1
e−x0(1 − x0 +		) = 0
	2

	3
e−x0(		− x0) = 0
	2

	3
Pochodna zmienia znak z + na − więc w x0 =		jest maksimum
	2

	3
Odp: (		, e−3/2 + 2)
	2

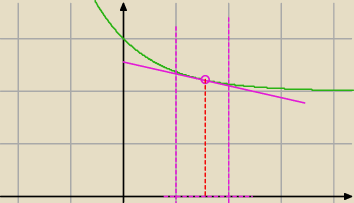===: ... możesz liczyć długo i namiętnie ... a możesz "z buta"

===: ...pole trapezu o danej wysokości jest maksymalne gdy średnia podstaw jest max

marek: Dzięki Wam!