W trojkacie prostokatny astrolog: W trojkacie prostokatnym dlugosci wysokosci i srodkowej poprowadzonej z wierzcholka kata prostego oraz dlugosc przeciwprostokatnej tworza ciag geometryczny, ktorego iloczyn wyrazow jest rowny 8. Oblicz promien okregu wpisanego w ten trojkat.

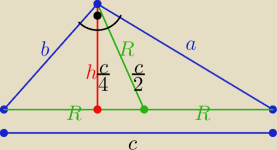
Eta: Fajne zadanko .... to rozwiążę

	c		c		1
c,		,		−−− tworzą ciąg geometryczny , c>0 , q=
	2		4		2

	c		c
c*		*		=8 ⇒ c3=64 ⇒ c=4 i 2R=4
	2		4

	ab
h=1		=h ⇒ ab= 8
	c

a²+b²=64 ⇒ (a+b)²−2ab=64 ⇒ (a+b)²=80 ⇒ a+b= 4√5 i 2R+2r=a+b ⇒ r= ....... = 2√5−4 [j] Powodzenia w następnych

Eta: Poprawiam chochliki ( bo liczyłam w pamięci) c=4 to h= 1 2R=4

ab
	=h ⇒ ab=4
c

a²+b²= 16 ⇒ (a+b)²−2ab= 16 ⇒ (a+b)²= 24 ⇒ a+b= 2√6 to 2R+2r= a+b ⇒ r=.... = √6−2 [j]

Eta: 2 godziny minęło ! a Ty ni be, ni me , ni pocałuj ...... Wrzucasz tylko coraz to nowe zadania