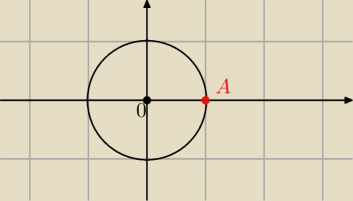
Izometrie13 5-latek: Zadanie nr 25 . Znajdz wspolrzedne obrazu punktu A=(1,0) w obrocie dookoła początku układu wspolrzednych o kąt a) 180^o to A'=(−1,0) b) 360^o to A'=A=(1,0) c) 90 ^o to A'=(0,1) d ) 45 ^o e) 30 ^o f) −135 ^o Teraz o ile a) b) c) to nie problem Jeśli chodzi natomiast o d) e) f) Chodzi o to czy mam te katy znaleźć za pomocą cyrkla i linijki bo kat 45 stopni to kat prosty podzielę na polowe i mam 45 stopni i jeśli znajde wspolrzedne obrazu punktu A w obrocie o 45 ^o to w symetrii srodkowej względem 0 będę mia wspolrzednie obrazu punktu w obrocie o kąt −135 ^o Natomiast kąt 30 stopni znajde wpisując okrag sześciokąt foremny (mam kąt 60^o dziele go na pol i mam kąt 30 ^o Czy tutaj chodzi o wykorzystanie własności trokątow 45,45 90 i 30 60,90 stopni Bo np. dla 45 stopni będziemy mieli trojkat prostokątny równoramienny i przeciwprostokątne dlugosci 1

5-latek: Teraz tak patrze i kat 45 stopni mogę znaleźć znacznie prościej rysując prosta y=x

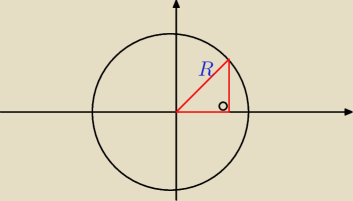
zombi: Zauważ, ze R jest niezmienne. Dla punktu (1,0) R=1, również jak przeniesiemy punkt o 45^o to R się nie zmieni, bo przenosimy punkt po okręgu. Nasz trójkąt ma kąty 45,45,90 i ma przeciw prostokątną równą R. To znajdziemy długości naszych dwóch przy prostokątnych a z tego już obie współrzędne.

5-latek: Witaj O to mi wlasnie chodzilo czy wykorzystać te trójkąty . dzięki

zombi: Ogólnie zachodzi tak. Jeśli obracamy punkt (x,y) względem punktu (0,0) o kąt α, to nowe współrzędne wyglądają tak: x' = xcosα − ysinα y' = xsinxα + ycosα A jeśli znamy liczby zespolone, to mając liczbę z = x+yi = (x,y), możemy przedstawić jej obrót o kąt γ względem punktu (0,0) w postaci trygonometrycznej wygląda tak: z' = z(cosγ+isinγ)

5-latek: Tak . Ja znam te wzory z liceum . Tylko to jest zadanie z 1 klasy LO i tych wzorow jeszcze nie było Luknij może na moje zadanie nr 26 . dzięki