ile jest liczb trzycyfrowych w których cyfra 3 występuje tylko raz? Hadasz: ile jest liczb trzycyfrowych w których cyfra 3 występuje tylko raz? Czy ktoś mógłby mi to wytłumaczyć? krok po kroku

wmboczek: 3xx − 81 x3x − 72 xx3 − 72

Hadasz: Tylko dlaczego?

Malina: Liczb trzycyfrowych jest ogółem; 9*10*10 (pierwsza cyfra nie moze byc 0 dlatego jest 9 a nie 10) a te ktore zawierają cyfrę trzy tylko raz moze byc 1) 9*9*9 (jesli bedzie cyfra 3 w setkach to w dziesiątkach i jednościach juz jej nie moze byc stąd 9) 2) 8*10*9 (jesli bedzie w dziesiątkach to nie moze byc w setkach i jednosciach) 3) 8*9*10 ( jesli bedzie w jednosciach to nie moze byc w setkach ani dziesiątkach) skad sie wzielo 9*10*10? Bo mozliwe sa cyfry do wyboru 0(tylko w dziesiątkach i jednostkach),1,2,3,4,5,6,7,8,9

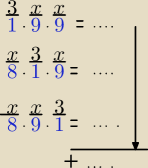
Eta: 1/ na pierwszym miejscu 3 ( 1 cyfra) na drugim i na trzecim ( po 9 cyfr bo bez trójki 2/ na pierwszym miejscu 8 cyfr( bez zera i bez trójki ) na drugim 3 ( 1 cyfra) na trzecim 9 cyfr ( bo bez trójki i z zerem) 3/ na pierwszym 8 cyfr( bo bez zera i bez trójki) na drugim 9 cyfr( bo tylko bez trójki i z zerem) na trzecim tylko 3 ( jedna cyfra) z reguły mnożenia : 1*9*9+8*1*9+8*9*1= .... takich liczb

Marika : Nie prawda! Masz tu rozpisane: 103,113,123,143,153,163,173,183,193 (9) 130;131,132,134,135,136,137,138,139 (9) 203,213,223,243,253,263,273,283,293 (9) 301...(100− 10= 90) 403... (9) 503... (9) 603...(9) 703...(9) 803...(9) 903...(9) 9*9+90=81+90=171

Mila: Dla Mariki http://liga.mat.umk.pl/rozw/rocznik91a/07_chwia/04_05_g1_liga1_07r/04_05_g1_liga1_07r.html

Eta:

PW: Liczbę trzycyfrową można utożsamić z ciągiem (a, b, c), w którym b, c ∊{0,1,2,3,4,5,6,7,8,9} i jednocześnie a ∊ {1,2,3,4,5,6,7,8,9}. Jeżeli dodatkowo założymy, że dokładnie jeden wyraz ciągu ma być cyfrą 3, to będę to ciągi typu: (1) (3, b, c) lub (2) (a,3, c) lub (3) (a,b,3}, w których b, c ∊{0,1,2,4,5,6,7,8,9} i jednocześnie a ∊ {1,2,4,5,6,7,8,9}. Ciągów typu (1) jest 9·9, ciągów typu (2) jest 8·9, ciągów typu (3) jest 8·9, razem 9(9+8+8) = 9·25 = 225. Piszę to samo co Eta, bo inaczej być nie może..

Wiktoria : ile jest liczb trzycyfrowych w których cyfra 6 występuje tylko raz?

getin: Zrobimy przeciwnie − policzymy ile jest liczb 3−cyfrowych w których cyfra 6: a) nie występuje w ogóle b) występuje dwa razy c) występuje trzy razy i zsumowaną ilość liczb z punktów a, b, c odejmiemy od 900 bo wszystkich liczb trzycyfrowych jest właśnie 900 a) 8*9*9 = 648 (cyfrę setek wybieramy ze zbioru {1,2,3,4,5,7,8,9}, cyfrę dziesiątek ze zbioru {0,1,2,3,4,5,7,8,9} i jedności też ze zbioru {0,1,2,3,4,5,7,8,9} b) wypisujemy liczby które mają dwie szóstki: 660, 661, 662, 663, 664, 665, 667, 668, 669 166, 266, 366, 466, 566, 766, 866, 966 606, 616, 626, 636, 646, 656, 676, 686, 696 Jest 26 takich liczb z dwoma cyframi 6 c) Jedna liczba 666 Odp. 900 − 648 − 26 − 1 = 225 liczb trzycyfrowych z jedną cyfrą 6

. : Getin − po co utrudniać sobie robotę? 1*9² + 2*8*1*9 = 9*(9 + 16) = 225 Czyli : '6' na pierwszym miejscu a pozostałe dowolne (byle nie 6) + inna na pierwszym, na jednym z pozostałych miejsc '6' (stąd to 2*1) i na ostatnim wolnym inna niż '6'

getin: Chciałem zrobić innym sposobem niż boczek na początku tematu z trzycyfrowymi liczbami z jedną cyfrą 3

. : Myślisz że Wiktoria chociaż przeczytała poprzednie wpisy? Nie sądzę.

getin: Też nie, ale może inni przeczytają − zobaczą że można tak albo tak zrobić zadanie