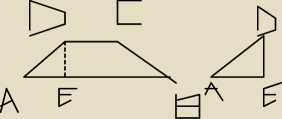
 W graniastosłupie prostym podstawą jest trapez równoramienny o podstawach długości 2 cm i 6 cm
oraz kącie ostrym 30 stopni. Wysokość tego graniastosłupa wynosi 4 cm.
Oblicz:
a) objętość graniastosłupa
b) długość przekątnej graniastosłupa
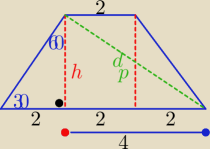
Wysokość podstawy trapezu będzie :
kąt EAD =30o
kąt AED=90o
więc kąt EDA=60o
W graniastosłupie prostym podstawą jest trapez równoramienny o podstawach długości 2 cm i 6 cm
oraz kącie ostrym 30 stopni. Wysokość tego graniastosłupa wynosi 4 cm.
Oblicz:
a) objętość graniastosłupa
b) długość przekątnej graniastosłupa
Wysokość podstawy trapezu będzie :
kąt EAD =30o
kąt AED=90o
więc kąt EDA=60o
| 2 | ||
no i z tego wynika że a√3=2 więc h(równe w tym wypadku a wyniesie h= | √3 ? | |
| 3 |
| a+b | 8 | 32 | ||||
V= | *h*H= | √3*4= | √3 | |||
| 2 | 3 | 3 |
| h | ||
Albo tg30o= | ||
| 2 |
| √3 | ||
h=2* | ||
| 3 |
| 2√3 | ||
h= | ||
| 3 |
| √3 | ||
h(trapezu)= | ||
| 3 |
| 4√3 | ||
Pp= | ||
| 3 |
| 16√3 | ||
V= | ||
| 3 |
| √3 | ||
d(trapezu}= √52+( | )2=............ | |
| 3 |

| √3 | ||
Skąd się bierze h= | .? | |
| 3 |
 Sorry .... masz dobrze
Sorry .... masz dobrze  Ja zamiast b= 2 zobaczyłam b=4
Ja zamiast b= 2 zobaczyłam b=4
| 2√3 | 32√3 | |||
zatem h= | jest ok i V= | też ok | ||
| 3 | 3 |
 Pozdrawiam i kolorowych x]
Pozdrawiam i kolorowych x]
