matematykaszkolna.pl
przebieg zmiennosci funkcji adi23: f(x)= x ln x Oblicz granice na krańcach dziedziny, funkcję rosnącą i malejącą i gdzie funkcja jest wypukła i wklęsła
9 gru 18:23
Janek191: D = < 0; +∞ )
9 gru 18:27
Janek191: Oblicz I i II pochodną.
9 gru 18:29
adi23: pierwsza lnx + 1 druga 1/x
9 gru 18:30
Janek191: Kiedy y ' = 0 ? , kiedy y ' < 0 ? kiedy y ' > 0 ?
9 gru 18:33
adi23: y'<0 to ma wyjść coś takiego x<e−1?
9 gru 18:39
adi23: y'=0 x=−1?
9 gru 18:42
Janek191: rysunek
 1 
y ' = 0 ⇔ x = e−1 =
 e 
 1 
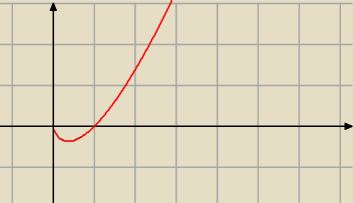
Dla x ∊ ( 0;
) jest f ' (x) < 0 , a dla x > U{1]{e} jest f' (x) > 0
 e 
więc
 1 1 
f maleje e ( 0;
) , rośnie w (
: + ∞)
 e e 
 1 
f − osiąga minimum dla x =
.
 e 
Dla x ∊ D f '' (x) > 0 , więc funkcja f jest wypukła w D
9 gru 18:44
Janek191: Tam powinno być ( 18.27 ) D = ( 0 ; + ∞ )
9 gru 18:47
adi23: Wielkie dzięki emotka
9 gru 18:47
adi23: Więc dziedzina funkcji przy zerze ma przedział otwarty?
9 gru 18:49
Janek191: Jeszcze granice na krańcach dziedziny .
9 gru 18:49
Janek191: Ze względu na logarytm.
9 gru 18:50
adi23: Ok a jak będzie z tymi granicami?
9 gru 19:02
Janek191: lim f(x) = + ∞ x→∞
9 gru 19:12
adi23: a przy granicy dążącej do 0?
9 gru 19:19
Janek191: Może tak: H
 − ln x 
−1 
x 
 
lim x *ln x = lim [ −
] = − lim
=
 
1 
x 
 
 1 
−
 x2 
 
x→0+ x→0+ x→0+ = lim − x = 0 x→0+
9 gru 19:20