proste gggg: Podaj wzór funkcji, której wykres otrzymano w wyniku przeksztalcenia paraboli o równaniu y= x² +4x−5 przez symetrię względem a)osi OX b)osi OY c)punktu O(0,0) d)prostej y=−5

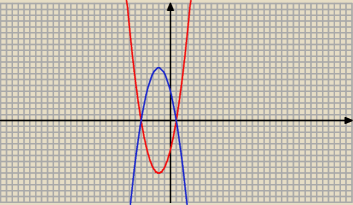
Janek191: a) y = − x² − 4 x + 5

gggg: ze co ?skad wzioles taki wzor nie chodzi o wykres

Janek191: y = − f(x)

olekturbo: b) y = f(−x) c y = −f(−x)

gggg: spoko tylko wytlumacz bo ja to wiem tylko ...np w b ma byc x²+4x+5 a dlaczego nie −x²

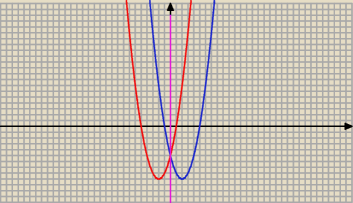
Janek191: b) P = ( x, y) więc P ' = ( − x , y) Mamy więc ( x ; y) → ( x' , y ') = ( − x ; y) Wstawiamy do wzoru: y = ( − x)² + 4*( − x) − 5 = x² − 4 x − 5 = f( − x)

gggg: a c i d?

Janek191: a, c − postępujemy w ten sam sposób co w b).

Janek191: d) Zapisujemy f w postaci kanonicznej. Wyznaczamy W, następnie W ' , itd.

gggg: hmm jakbym jescze rozumial d

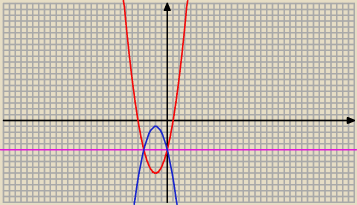
Janek191: W = ( p; q )

	− 4
p =		= − 2
	2

q = f(p) = f(−2) = ( −2)² + 4*(−2) − 5 = 4 − 8 − 5 = − 9 więc W = ( − 2, − 9) y = ( x + 2)² − 9 ; a = 1 S = ( − 2 ; − 5) − środek odcinka W W' ; W ' = ( − 2 , y ') więc

− 9 + y '
	= − 5
2

− 9 + y ' = − 10 y ' = − 1 W ' = ( − 2; − 1) zatem a ' = − 1 y = − ( x + 2)² − 1 = − ( x² + 4 x + 4) − 1 = − x² − 4 x − 5 Odp. y = − x² − 4 x − 5 ==================== Patrz też na wykres

gggg: no moze pomysle nad tym ale dziekuje bardzo

Janek191: a, b, c − widać od razu d) − trochę bardziej skomplikowane

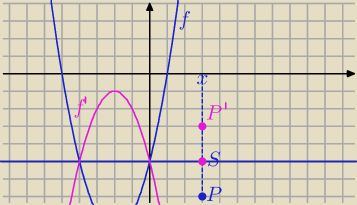
Mila: y= x² +4x−5 d) symetria względem prostej y=−5 Można znaleźć ogólny wzór przekształcenia albo Znaleźć obraz wierzchołka paraboli napisać wzór paraboli w postaci kanonicznej, parabola będzie skierowana w dół, a'=−1 W=(−2,−9) poniżej osi symetrii, w odległości od osi: |−9−(−5)|=4 W'=(−2, −9+8)=(−2,−1) Szukamy wzoru: a'=−1 f(x)=−1*(x+2)²−1 f(x)=−1*(x²+4x+4)−1 f(x)=−x²−4x−5 ==================

gggg: dziekuje