Trygonometria Jasiu: sinx+cosx=−1 sinx+sin(^π₂)=−1 => cosx=sin(90°−x) 2sin^x+π/2−x₂*cos^x−π/2+x₂=−1 => wzór na sumę sinusów (zapisałbym z ^._. ale coś się popsuło sin^π₂*cos(x−^π₄)=−1 =>redukcja co mam z tym zrobić dalej? trochę sie pogubiłem...

Mila:

	π
sin(x)+sin(		−x)=−1
	2

	π		π
2*sin		*cos(x−		)=−1
	4		4

	√2		π
2*		*cos(x−		)=−1⇔
	2		4

	π		1
cos(x−		)=−		⇔
	4		√2

	π		√2
cos(x−		)=−
	4		2

	π		π		π		π
x−		=		+π+2kπ lub x−		=−		+π+2kπ teraz dokończ
	4		4		4		4

Jasiu: nie wiem skąd wziełaś: x−^π₄=^π₄+π+2kπ ja bym napisał: x−^π₄=^π₄+2kπ

Jasiu: wyniki: x=2kπ ⋁ x=^π₂+2kπ ale w odpowiedzach jest inaczej... nie wiem gdzie błąd

Mila: Jasiu rozwiąż takie równanie :

	1
cosx=−
	2

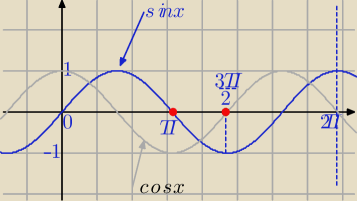Mila: To rozwiązanie które podałeś z odpowiedzi pasuje do równania: sinx+cosx=1 ============================================== Do równania, które podałeś jest takie jak napisałam, ale nie dokończyłeś: (?) sinx+cosx=−1

	π		π		π		π
x−		=		+π+2kπ lub x−		=−		+π+2kπ⇔
	4		4		4		4

	π
x=		+π+2kπ lub x=π+2kπ
	2

	3π
x=		+2kπ lub x=π+2kπ
	2

spr.

	3π		3π
L=sin(		)+cos		=−1+0=−1=P
	2		2

L=sin(π)+cos(π)=0+(−1)=−1=P