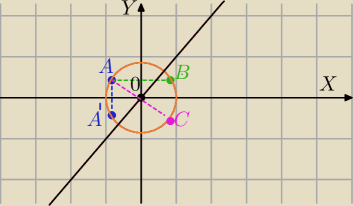
Izometria 11 5-latek: Zadanie nr 19. Ja tego nie rozumiem naprawdę Jeśli mam okrag o srodku w początku układu wspolrzednych i dowolnym promieniu to jego obrazem w symetii S_x będzie ten sam okrag (dlaczego ? Dlatego ze obrazem punktu A w symetrii wzgledm osi OX będzie punkt A' a obrazem punktu A' w symetrii względem osi OX będzie punkt A ? Obrazami punktów na przeciu się z osia OX będą te same punkty To samo będzie w symetrii S_y Tez obrazem rego okręgu będzie ten sam okrag bo obrazem punktu A w symetrii względem osi OY będzie punkt B a obrazem punktu B w symetrii względem osi OY będzie punkt A Punty przecięcia się okręgu z osia OY sa punktami stalymi Dobre to jest tłumaczenie ? Natomiast nie mogę sobie wyobrazić dlaczego obrazem okegu względem punktu 0 jest ten sam okrag . czy może dlatego ze jest to punkt staly przekształcenia ? Zrobilem jeszcze rysunek do zadania Tresc zadania : ============== Czy tylko z postaci równania bez korzystania z własności okręgu i jesgo średnicy widzisz ze obrazem okręgu x²+y²=1 w symerii względem prostej y=x jest on sam . Jakie jeszcze symetrie okręgu widzisz zsamego równania . Najpierw chciałbym wyjasnic to co pisałem na początku . Bardzo dużo mi to wyjasni do tego zadania

Mila: Symetria jest izometrią. zatem r'=r=1 Obrazem punktu S=(0,0)jest ten sam punkt, bo należy do osi symetrii. Okrąg ma nieskończenie wiele osi symetrii. Każda prosta y=ax, a∊R i prosta x=0 jest osią symetrii okręgu o równaniu x²+y²=1.

5-latek: Dziekuje Ci A to dla symetrii S_x i S_y do dobre tłumaczenie ?

Mila: A jakie masz wątpliwości?

5-latek: Już nie mam . Tak będzie