 Zadanie nr 18
Napisz równanie prostej przechodzącej przez punkty A= (1,9) i B=(2,2) oraz równanie jej
obrazu względem prostej y=x Narysuj obie proste
Rownanie prostej przechodzącej przez A i B
Zadanie nr 18
Napisz równanie prostej przechodzącej przez punkty A= (1,9) i B=(2,2) oraz równanie jej
obrazu względem prostej y=x Narysuj obie proste
Rownanie prostej przechodzącej przez A i B
| 2−9 | y−9 | ||
= | |||
| 1 | x−1 |

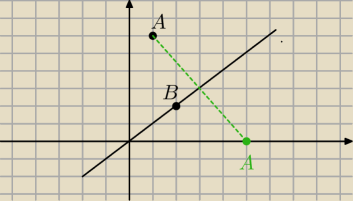 Cześć małolat .. .trochę kombinujesz , jak koń pod górę .. patrz na rysunek
....szukasz obrazu punktów A i B w symetrii osiowej wzgledem prostej: y = x
( punkty: A' i B') i piszesz równanie prostej przechodzącej przez A' i B'
( tutaj tak się złozyło,że: B = B' , ale zasada jest taka sama dla innych punktów)
Pozdrawiam (J)
Cześć małolat .. .trochę kombinujesz , jak koń pod górę .. patrz na rysunek
....szukasz obrazu punktów A i B w symetrii osiowej wzgledem prostej: y = x
( punkty: A' i B') i piszesz równanie prostej przechodzącej przez A' i B'
( tutaj tak się złozyło,że: B = B' , ale zasada jest taka sama dla innych punktów)
Pozdrawiam (J) 
 Jakie piękne proste rozwiązanie . A ja faktycznie kombinuję
Jakie piękne proste rozwiązanie . A ja faktycznie kombinuję  Dziekuje
Dziekuje
 Pozdrawiam
Już to wiem .
Co do postu z 01:11 to zasugerowałem się zadaniem nr 14 (gdzie osia symetrii dla dwóch
przecinających się prostych była dwusieczana miedzy tymi prostymi . Dlatego napisałem o tej
dwusiecznej
Pozdrawiam
Już to wiem .
Co do postu z 01:11 to zasugerowałem się zadaniem nr 14 (gdzie osia symetrii dla dwóch
przecinających się prostych była dwusieczana miedzy tymi prostymi . Dlatego napisałem o tej
dwusiecznej