Wyznacz przedziały monotoniczności i ekstrema lokalne funkcji Efka: Wyznacz przedziały monotoniczności i ekstrema lokalne funkcji 1) f(x)=x² lnx Pochodna mi wyszła 2xlnx + x ( dobrze ?) i w sumie nie wiem co tu później mam zrobić wydaje mi się, że pochodną muszę do 0 przyrównać i wtedy mam lnx=−1/2 i tu się zatrzymuje. 2) f(x)=(x² − 2x)^2/3 Pochodna = 2/3(2x−2)^−1/3 I dalej znowu klops... 3) f(x)=(lnx)² − 2lnx A tu już kompletnie nie wiem Pomoże ktoś ?

Efka: w 3 pochodna chyba f'(x)=2lnx − 2/x

J:

	2
3) f'(x) = 2lnx/x − 2/x =		(lnx − 1)
	x

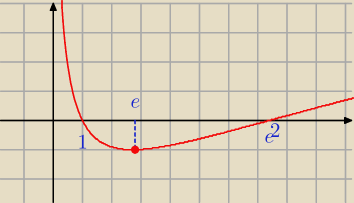
Janek191: 3) cd. f(x) = ( ln x)² − 2 ln x ; x > 0

	2
f '(x) = 0 ⇔		*( ln x − 1) = 0 ⇔ ln x = 1 ⇔ x = e
	x

Dla x < e jest f '(x) < 0 , a dla x > e jest f '(x) > 0 , więc funkcja f w punkcie x = e osiąga minimum lokalne y_min = f(e) = 1² − 2 = − 1 oraz f maleje w przedziale ( 0 ; e ), a rośnie w ( e; + ∞ ) f(x) = 0 ⇔ ( ln x)² − 2 ln x = 0 ⇔ ( ln x)*( ln x − 2) = 0 ⇔ ln x = 0 lub ln x = 2 ⇔ ⇔ x = 1 lub x = e²

Jerzy: 1) f'(x) = x(2lnx + 1)

	1		1
f'(x) = 0 ⇔ lnx = −		⇔ x =		i pochodna zmienia znak, zatem:
	2		√e

	1		1
w punkcie: x =		funkcja osiąga minimum , jest malejąca w przedziale (0,		)
	√e		√e

	1
i rosnaca w (		,+∞)
	√e

Jerzy: 2) f'(x) = 2/3(x² − 2x)^−1/3(2x − 2) f'(x) = 0 ⇔ x = 1 i pochodna zmienia znak ..... wnioski ?