Policz ekstremum i monotoniczność. f(x)=x^3*e^-x
Morela: Policz ekstremum i monotoniczność.
f(x)=x3*e−x
Pochodna wychodzi e−x (3x2−x3)
Jak z tego policzyć ekstremum?
Janek191:
f(x) = x
3*e
−x
więc
f '(x) = 3 x
2*e
−x + x
3* ( − e
−x) = e
−x*( 3 x
2 − x
3) = 0 ⇔ 3 x
2 − x
3 = 0 ⇔
⇔ x
2*( 3 − x) = 0 ⇔ x = 0 lub x = 3
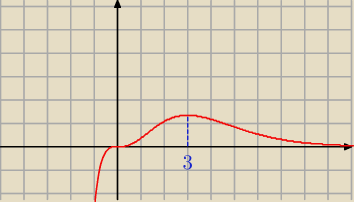
Dla x < 0 jest f '(x) > 0 , a dla x > 0 jest f '(x) > 0 − nie ma ekstremum
Jest punkt przegięcia ( trzeba to sprawdzić )
Dla x < 3 jest f '(x) > 0, a dla x > 3 jest f' (x) < 0 − maksimum funkcji f
oraz
f rośnie w ( −
∞ , 3) oraz f maleje w ( 3 ; +
∞ )
 f(x) = x3*e−x
więc
f '(x) = 3 x2*e−x + x3* ( − e−x) = e−x*( 3 x2 − x3) = 0 ⇔ 3 x2 − x3 = 0 ⇔
⇔ x2*( 3 − x) = 0 ⇔ x = 0 lub x = 3
Dla x < 0 jest f '(x) > 0 , a dla x > 0 jest f '(x) > 0 − nie ma ekstremum
Jest punkt przegięcia ( trzeba to sprawdzić )
Dla x < 3 jest f '(x) > 0, a dla x > 3 jest f' (x) < 0 − maksimum funkcji f
oraz
f rośnie w ( − ∞ , 3) oraz f maleje w ( 3 ; +∞ )
f(x) = x3*e−x
więc
f '(x) = 3 x2*e−x + x3* ( − e−x) = e−x*( 3 x2 − x3) = 0 ⇔ 3 x2 − x3 = 0 ⇔
⇔ x2*( 3 − x) = 0 ⇔ x = 0 lub x = 3
Dla x < 0 jest f '(x) > 0 , a dla x > 0 jest f '(x) > 0 − nie ma ekstremum
Jest punkt przegięcia ( trzeba to sprawdzić )
Dla x < 3 jest f '(x) > 0, a dla x > 3 jest f' (x) < 0 − maksimum funkcji f
oraz
f rośnie w ( − ∞ , 3) oraz f maleje w ( 3 ; +∞ )