Pomocy pochodna. Sztefan: Obliczu e ekstrema oraz największą i najmniejsza wartość funkcji ^(x2+1)_(x²−4)

Jerzy: i co proponujesz ?

Janek191: Przepisz wzór funkcji przy użyciu litery U

	x2 + 1
Czy f(x) =		?
	x2 − 4

Sztefan: Tak policzyłem i wyszło mi ze brak ekstremów i x1 =0

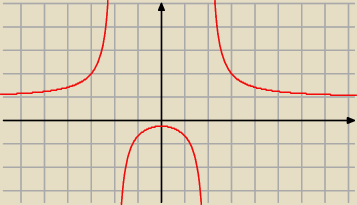
Janek191: f ma ekstremum − maksimum lokalne

Jerzy: no to źle Ci wyszło ... funkcja ma ekstremum lokalne

Sztefan: Jakim cudem funkcja ma ekstremum lokalne przy 1 miejscu zerowym? Myślałem ze istnieje zasada iz funkcja ma o 1 mniej ekstremum niż miejsc zerowych

Sztefan: Tzn tak ma maksimum w f(0) ale czy ma ekstrema?

Janek191: Ta funkcja nie ma miejsc zerowych

Janek191: Wykres funkcji f nie przecina osi OX

Jerzy: f(0) to przecież maksimum lokalne

Janek191: Oblicz pochodną funkcji f .

Sztefan: http://m.wolframalpha.com/input/?i=%28x%5E2%2B1%29%2F%28x%5E2-4%29&x=1&y=3

Sztefan: Obliczyłem pochodna wiem jak liczymy pochodna z ułamka ale wychodzi wielomian 4 stopnia w mianowniku nieskracalny

Jerzy: i czego ciekawego się dowiedziałeś z tego linku ?

Jerzy:

	−10x
bzdura f'(x) =
	(x2 − 4)2

Janek191: Mianownik nie jest potrzebny do wyznaczenia ekstremum ale licznik ( = 0 )

Jerzy: co Cię obchodzi mianownik ... kiedy ta pochodna się zeruje i jak zmienia znak ?

Sztefan: Tak i jak teraz wyliczymy z tego ekstrema bez miejsc zerowych?

Sztefan: Zeruje się przy x=0?

Jerzy: tak ... i teraz jak zmienia znak ?

Sztefan: W zależności od wartości x w liczniku?

Janek191: f '(0) = 0 Dla x < 0 jest f '(x) > 0 to f rośnie Dla x > 0 jest f ' (x) < 0 to f maleje czyli w x = 0 funkcja f ma maksimum lokalne.

Sztefan: Aha... Rozumiem ale teraz jak powinienem wyliczyć ich wartość bo takiego przykładu bez jasnych miejsc zerowych jeszcze nie robiłem?

Sztefan: Oczywiście wartość ekstrem

Jerzy: ta funkcja nie ma miejsc zerowych

Jerzy: f_max = f(0)

Sztefan: Wiem ze niema ale czy ma ekstrema jeżeli tak to jak je policzyć bez miejsc zerowych?

Sztefan: Chyba wiec czegoś ciągle nie rozumiem...

Jerzy:

	02 + 1		1
max = f(0) =		= −
	02 − 4		4

Sztefan: To zadanie jest wprost wyjęte z mojego sprawdzianu w zad jest Obliczu ekstrema lokalne orz wartości najmniejsze i najwieksze . Wiec mam fmax = −1/4 a co z najmniejsza i ekstrema mi?

Jerzy: nie ma wartości najmniejszej , ani najwiekszej

Sztefan: Dobra kompletnie nic nie rozumiem zajrze do teorii i sprobuje ogarnąc. Tak czy inaczej dzieki

Sztefan: Myślałem ze właśnie najwieksa wartość to −1/4 a ekstrema i najmniejsza nie istnieje.