zadanie geometria analityczna daimos0: Witam! Potrzebuje pomocy z rozwiązaniem poniższego zadania. Jak krok po kroku je rozwiązać. Kolejne wierzchołki równoległoboku ABCD mają współrzędne : A=(−6−2√2,4+6√2) , B=(−2−√2, 6+2√2) , C=(4+6√2, −2−2√2) . Wyznacz współrzędne punktu przecięcia się przekątnych równoległoboku A'B'C'D' który jest obrazem równoległoboku ABCD w symetrii względem osi OY. Proszę o pomoc pilne! Dziękuje

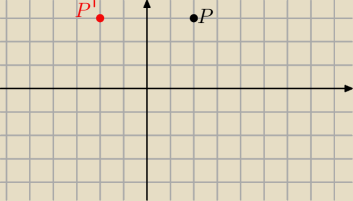
5-latek: Chopie o tej godzinie Widzisz ze obrazem punktu P o wspolrzednych (x,y) jest punkt P' o wspolrzednych (−x.y)

daimos0: Tak to wiem jak symetria wygląda tylko chodzi o to że nie umiem tego obliczyć i skorzystać z podglądowego rysunku, nie mogę sobie tego wyobrazić

5-latek: wezmy punkt A = (−6−2√2,4+6√2 ) lezy on w drugiej cwiatce Wiec punkt A' który jest obrazem punktu A będzie miał wspolrzedne A'=(−(−6−2√2), 4+6√2) to A'=(6+2√2, 4+6√2) (będzie lezal w 1 ćwiartce Punkt B=(−2−√2),6+2√2) tez lezy w 2 ćwiartce bo (−2−√2)<0 a 6+2√2>0 Wiec punkt B ' który jest obrazem punktu B ma wspolrzedne B'=(−(−2−√2 , 6+2√2) to B'= (2+√2, 6+√2}

5-latek: Za szybko wyslalem Punkt C jak widzisz lezy w 4 ćwiartce wiec punkt C' który jest obrazem punktu C będzie lezal w 3 ćwiartce i będzie miał wspolrzedne C'=(−(4+6√2,−2−√2) to C'=(−4−6√2, −2−√2 ) Weź teraz sobie zrob rysunek (przyjnij √2≈1,41 i zanacz te punkty Będzie to takoi rysunek poglądowy Zobaczysz czy jedna z przekątnych to A'C' jeśli tak to srodek odcinka A'C' jest punktem przecięcia przekątnych

daimos0: Zrobiłem tak , naniosłem wierzchołki na podglądowy rysunek , ale wychodzi bardzo dziwny ten równoległobok , punkty A B C wychodzą prawie w jednej linii , no i automatycznie A' B' C' też symetrycznie w jednej linii , i ta linia przecina się gdzieś w punkcie (0, 6) jednak z rysunku ciężko to dokładnie okreslić. Strasznie dziwny ten przykład..

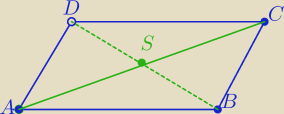
Mila: W równoległoboku przekątne dzielą się na połowy. Punkt przecięcia przekątnych jest środkiem symetrii równoległoboku. S jest środkiem AC. A=(−6−2√2,4+6√2) , B=(−2−√2, 6+2√2) , C=(4+6√2, −2−2√2) S(x_s,y_s):

	xa+xc		−6−2√2+4+6√2
xs=		=		=−1+2√2
	2		2

	ya+yc		4+6√2−2−2√2
ys=		=		=1+2p{2]
	2		2

S=(−1+2√2,1+2√2) W symetrii względem OY otrzymamy S'=(−(−1+2√2),1+2√2)=(1−2√2,1+2√2)