Równoległobok brunatny: Krótsza przekątna równoległoboku wynosi 2√5cm i tworzy z krótszym bokiem kąt prosty. Stosunek długości boków równoległoboku jest równy 2 i 3. Oblicz pole, obwód i drugą przekątną równoległoboku. Da się to zadanie rozwiązać z wiedzą gimnazjalną?

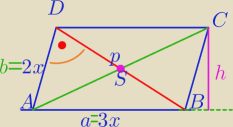
Mila: x− wspólna miara, x>0 p=2√5 W ΔADB: a²=p²+b² (3x)²=(2√5)²+(2x)² 9x²=20+4x² 5x²=20 x²=4 x=2 a=3*2=6 b=2*2=4

	1		1
PΔABD=		p*b=		*2√5*4=4√5
	2		2

P{ABCD}=2*4√5=8√5 ob=2*(6+4)=20 AS, potem AC oblicz sama.

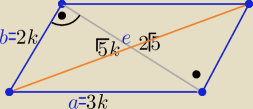
Eta: e= √9k²−4k²= √5k = 2√5 ⇒ k=2 to a=6 , b= 4 obwód L= 2a+2b= 20

	1
P= 2*P(ΔABC) = 2*		b*e= 4*2√5= 8√5
	2

f²+e²= 2a²+2b² ⇒ f²= 72+32 −20 ⇒ f=√84= 2√21