nierowność
Metis: Mogę szybciej rozwiązań taką nierównośc niż rozbijać ją na przypadki?
| | 2x | |
−1< |
| <1 /(*(x2−3)2 itd? |
| | x2−3 | |
Dodam, że chodzi o szereg geometryczny.
6 gru 16:49
sushi_gg6397228:
mozna dłużej
|2x| < |x2−3|
i zrobić rysunki lewa strona i prawa strona osobno
6 gru 16:52
Mila:
Dobrze zacząłeś.
6 gru 16:53
Metis: Dobry wieczór [R[Milu]].
Ciągnąc dalej :
−(x
2−3)
2<2x<(x
2−3)
2
2x<(x
2−3)
2 i 2x>−(x
2−3)
2
I w tym momencie wchodzę na nierówności wielomianowe, to jedyna droga, oprócz graficzej
sushiego ?
6 gru 16:58
Metis: *
Milu 
6 gru 16:59
Jack: Raczej tak...
6 gru 16:59
sushi_gg6397228:
u mnie mozna zrobic przedziały 3 warianty i liczyc trzy nierownosci stopnia 2 (aby pozbyć sie
wartosci bezwzglednej)
6 gru 17:00
Metis: Zjadłem jeden czynnik.
6 gru 17:01
Metis: −(x2−3)2<2x(x2−3)<(x2−3)2
6 gru 17:02
Metis: Aż prosi się, aby skrócić przez (x2−3)2
6 gru 17:07
Metis: *(x2−3)
6 gru 17:08
Mila:
Wg wskazówki
sushi
|2x|<|x
2−3| /
2
4x
2<x
4−6x
2+9⇔
x
4−10x
2+9>0
łatwo się rozkłada .
Ja osobiście nie lubię mnożyć przez kwadrat mianownika .
Moje rozwiązanie:
| 2x | | 2x | |
| >−1 i |
| <1, x≠√3 i x≠−√3 |
| x2−3 | | x2−3 | |
| 2x | | 2x | |
| +1>0 i |
| −1<0⇔ |
| x2−3 | | x2−3 | |
| 2x+x2−3 | | 2x−x2+3 | |
| >0 i |
| >0 |
| x2−3 | | x2−3 | |
Unikasz komplikacji z wielomianami 4 stopnia , bo licznik rozkładasz i mianownik
6 gru 17:11
Metis: Dziękuje
6 gru 17:13
Mila:
6 gru 17:17
ICSP: (2x − x
2 + 3)(2x +x
2 − 3) < 0
(x
2 − 2x − 3)(x
2 + 2x − 3) > 0
(x− 3)(x+1)(x+3)(x−1) > 0
x ∊ (−
∞ ; −3) ∪ (−1 ; 1) ∪ (3 ; +
∞)
6 gru 17:20
Mila:
17:11 w ostatniej , druga nierówność ma byc znak "<", to pewnie zauważyłeś.
6 gru 17:50
52: ICSP czemu nie poszedłeś na matematykę
?
6 gru 19:01
ICSP: To nie dla mnie
6 gru 19:05
Metis: U
ICSP już pewnie dawno na ścianie wisi dyplom z matematyki
... tylko się nie chwali
6 gru 19:08
52: Pewnie tak... Wstydzi się przyznać
6 gru 19:10
Metis: Nie chce wyjść mi wynik taki jak u ICSP.
Z pierwszej nierówności otrzymuje :
x∊(−∞, −3) U (−√3, 1) U (√3,+∞)
Z drugiej :
x∊(−√3, −1) U (√3,3)
Część wspolna:
x∊(−√3, −1) U (√3,3)
6 gru 19:41
Metis:
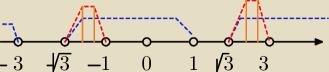
6 gru 19:48
Metis: Gdzie bład
6 gru 20:09
Metis: Bład znalezniony, zjadlem −
6 gru 20:40
Mila:
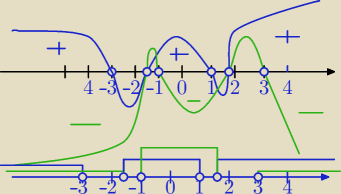
(2x+x
2−3)*(x
2−3)>0 i (−x
2+2x+3)*(x
2−3)<0⇔
(x+3)*(x−1)*(x+√3)*(x−√3)>0 i (x+1)*(x−3)*(x−
√3*(x+
√3)<0
−3,−√3,1,√3
−√3,−1,√3,3
część wspólna
x∊(−
∞,−3)∪(−1,1)∪(3,
∞)
6 gru 20:41
ICSP: Nie lepiej moim sposobem ?
6 gru 20:41
Metis: Dziekuje Milu. szkoda, że musiała się Pani tyle wyrysować. W mojej postaci iloczynowej
zjadłem minusa.
6 gru 20:43
Metis: ICSP wszystkie drogi prowadzą do Rzymu
6 gru 20:47
Mila:
Też zjadłam minusa w zapisie iloczynowym , ale rysowałam wg poprzedniej linijki.
Lepiej
ICSP, ale oglądam film i piszę, to nie myślę.
6 gru 21:01