Rozwiąż nierówność 2cos2x≤-1 w przedziale <-π,π> Paweł: Rozwiąż nierówność 2cos2x≤−1 w przedziale <−π,π>

M:

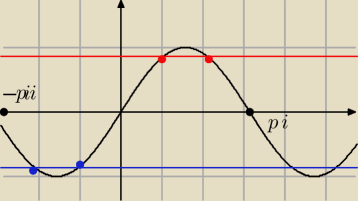
Xia Qingxue: 2cos2x≤−1 D=ℛ 2(cos²x−sin²x)≤−1 2cos²x−2sin²x≤−1 2(1−sin²x)−2sin²x≤−1 2−2sin²x−2sin²x≤−1 −4sin²x≤−3

	3
sin2x≥
	4

Teraz tak

	√3		√3
sinx≥		lub sinx≤−
	2		2

W przedziale [−π.π]

	√3
sin(x)≥
	2

	π		2π
x∊[		,		]
	3		3

W przedziele [−π,π] sinx≤−√3}{2}

	2π		π
x∊[−		.−		]
	3		3

	2π		π		π		2π
Odp: x∊[−		,−		]U[		,		]
	3		3		3		3

Prosze sprawdzić

Xia Qingxue: Wobec tego takie mam pytanie Mam taka nierówność(ogólnie ) 1)sin²x≥k Wobec tego mogę zapisać |sinx|≥√k stąd sinx≥√k lub sinx≤−√k ? Albo 2) sin²x≤q Tak samo |sinx|≤√q stąd sinx≤√q i sinx≥−√q? Czy lepiej w obu przypadkach nie uzywąć wartosci bezwzględnej ?

Xia Qingxue: Moje pytanie jest nadal aktualne.dziękuje