Ciągi+Trygonometria.
Ewka: Rozwiąż nierówność 1 + tgx + tg2x+.....<9+3√36
Jestem tutaj
11−tg(x)<3+√33
5 gru 19:34
sushi_gg6397228:
dziedzina, założenia

5 gru 19:38
Jack: skoro "jesteś tutaj"
to rozumiem, że lewą stronę określiłaś z szeregu geometrycznego i znasz dziedzinę owego szeregu
?

5 gru 19:40
Ewka: Czyli co mam napisać tgx ≠ 1?
5 gru 19:41
Ewka: i |q| < 1?
5 gru 19:42
Jack: skoro cosx jest w mianowniku to nie moze byc zerem
czyli
cos x ≠ 0
A ta lewa strone sprowadzilas do szeregu czy jak ? : D
5 gru 19:43
Jack: tak, dziedzine szeregu okresla sie za pomoca
|q| < 1
i dopiero wtedy mozesz cokolwiek liczyc... : )
5 gru 19:44
Ewka: No ale jak mam policzyć |tgx| < 1.
5 gru 19:51
sushi_gg6397228:
zrobić wykres tgx a potem |tgx|
5 gru 19:54
Jack: albo tak jak sushi mowi, albo
tg x > −1 i tg x <1
tg x + 1>0 i tg x − 1 <0
5 gru 19:58
Jack: aczkolwiek |tgx| < 1
latwo narysowac...
wiec jak idzie?

5 gru 20:22
Jack:
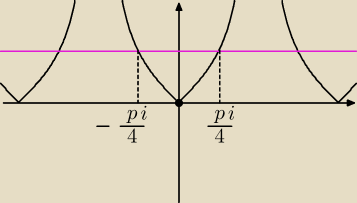
5 gru 20:45
Jack: | | −π | | π | |
x ∊ ( |
| + kπ ; |
| + kπ) |
| | 4 | | 4 | |
5 gru 20:47
Ewka: No tak to rozumiem ,ale potem interesuje mnie jak mam tą nierówność przekształcić przy
rozwiązywaniu
5 gru 21:06
5 gru 21:37
Jack:
2 = 3+
√3 (1−tg(x))
2 = 3+
√3 − tg x (3+
√3)
tg x (3+
√3) =
√3 + 1
Usuwanie niewymiernosci... :
| | √3 + 1 | | 3−√3 | | 3+2√3−3 | | 2√3 | | √3 | |
tg x = |
| * |
| = |
| = |
| = |
| |
| | 3+√3 | | 3−√3 | | 9−3 | | 6 | | 3 | |
a to już powinnaś wiedzieć : D
5 gru 21:43
Ewka: Czy przy nierównosciach zawsze mogę mnożyć na krzyż nawet w przypadaku −tg(x)?
5 gru 21:45
Jack: a Nie, nie mozna na krzyz...ehh, nawet nie zauwazylem ze to jest nierownosc, przepraszam
bardzo
5 gru 21:46
Ewka: tzn można gdy masz wszystko dodatnie
5 gru 21:47
Jack: no tak, tak , ale tu nie ; D
No to wszystko na jedna strone...i liczymy
5 gru 21:47
Jack: Dochodzę do takiej postaci... :
| −1 + 3tg(x) − √3(1−tg(x)) | |
| < 0 |
| 1−tg(x) | |
inaczej można zapisać
| | 2tg(x) | |
−1 − √3 + |
| < 0 |
| | 1−tg(x) | |
ale więcej Ci nie powiem

5 gru 22:05
sushi_gg6397228:
jakie było założenie −−−> |tg x| <1 <=> −1 < tg x <1 wiec 1− tgx jest liczbą dodatnią
zatem
na potrzeby zadania y= tg x
2 < (3+
√3 ) (1−y) \ : (3+
√3 )
| 2 | |
| < 1−y przenosze "y" na lewo , a ułamek na prawo |
| 3+√3 | |
| | 2 | |
y < 1 − |
| usuwam niewymiernosc |
| | 3+√3 | |
| | 2 (3−√3 ) | |
y < 1− |
| robie porzadki |
| | 6 | |
robie wykres tg x i odczytuje przedziały + uwzgledniam załozenia z dziedziną
6 gru 09:57




