
 →
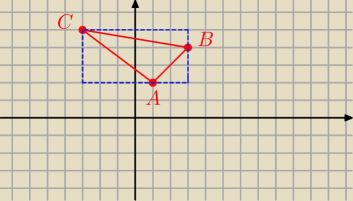
AB = [ 3 − 1; 4 − 2] = [ 2 ; 2]
→
AC = [ − 3 − 1; 5 − 2] = [ − 4; 3}
więc pole Δ ABC jest równe
→ →
P = I 0,5 *det ( AB , AC ) I = I 0,5*( 2*3 − (−4)*2) I = I 0,5*14 I = 7
→
AB = [ 3 − 1; 4 − 2] = [ 2 ; 2]
→
AC = [ − 3 − 1; 5 − 2] = [ − 4; 3}
więc pole Δ ABC jest równe
→ →
P = I 0,5 *det ( AB , AC ) I = I 0,5*( 2*3 − (−4)*2) I = I 0,5*14 I = 7
| 1 | ||
S = |xb, yb, 1| = | |xayb+xbyc+xcya−xcyb−xayc−xbya| = | |
| 2 |
