POMOCY ! WEKTORY !
:): Obliczyć długość wysokości trójkąta o wierzchołkach A(1, 2, 3), B(−1, 0, 1) i C(2, −1, 0),
poprowadzonej z wierzchołka A.
Prosiłabym o rozwiązanie, żebym mogła się połapać i jakoś do tego dojść, czemu tak

z góry dziękuję !

5 gru 14:38
Przemysław: Narysuj sobie w układzie współrzędnych te wierzchołki.
Możesz wtedy policzyć wszystkie długości boków.
Jest wzór pozwalający policzyć pole trójkąta z długości boków.
Następnie zauważ, że pole jest równe też 1/2*hBC*|BC|
Powinno wyjść
5 gru 14:52
:): ok spróbuję

dzięki !

5 gru 15:01
:): nie wyszło

5 gru 15:53
:): nie wiem czy dobrze policzyłam sinus α, bo chciałam też posłużyć się wzorem 1/2 absinα
5 gru 15:54
Przemysław: Dopiero zobaczyłem, że to 3D, a ja Ci kazałem rysować

A(1, 2, 3), B(−1, 0, 1) i C(2, −1, 0)
To może tak, policzę długości boków:
|AB|=
√(1−(−1))2+22+(3−1)2=
√4+4+4=
√12
|AC|=
√(1−2)2+32+32=
√1+9+9=
√19
|BC|=
√(−3)2+(−1)2+12=
√9+1+1=
√11
Teraz żeby nie myśleć za dużo, to:
https://pl.wikipedia.org/wiki/Wz%C3%B3r_Herona
i z tego mamy pole P.
A wysokość:
oczywiście mogłem się pomylić
5 gru 16:09
5-latek: Przemek a dlaczego np. ma nie narysować w układzie wspolrzecnych tych punktów ?
5 gru 16:11
Przemysław: No nie wiem. Można narysować, ale w trójwymiarze to trochę ciężko. I tylko dlatego w sumie.
Przynajmniej mi by raczej to nie pomoglo.
5 gru 16:13
5-latek:
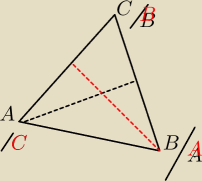
Ja bym jednak zrobil rysunek
gdyż np. jeśli przyjmiemy czarne ozbaczenie to wysokość będzie odlegloscia punktu A od
prostej BC
natomiast jeśli będzie oznaczenie takie jak czerowne to odleglosc punktu A tez będzie
odlegloscia od nowej BC tylko ze nowa BC to stara AC i ma inne równanie
Myle ze wiesz o co chodzi .
Natomiast ja tez mogę się w tym mylic

5 gru 16:23
Przemysław: Ale tak jak pisałem powinno wyjść.
Chociaż obliczenia trochę głupie będą z tym polem.
5 gru 16:24
:): dziękuje

!
5 gru 21:35
 z góry dziękuję !
z góry dziękuję ! 
 dzięki !
dzięki ! 

 A(1, 2, 3), B(−1, 0, 1) i C(2, −1, 0)
To może tak, policzę długości boków:
|AB|=√(1−(−1))2+22+(3−1)2=√4+4+4=√12
|AC|=√(1−2)2+32+32=√1+9+9=√19
|BC|=√(−3)2+(−1)2+12=√9+1+1=√11
Teraz żeby nie myśleć za dużo, to:
https://pl.wikipedia.org/wiki/Wz%C3%B3r_Herona
i z tego mamy pole P.
A wysokość:
A(1, 2, 3), B(−1, 0, 1) i C(2, −1, 0)
To może tak, policzę długości boków:
|AB|=√(1−(−1))2+22+(3−1)2=√4+4+4=√12
|AC|=√(1−2)2+32+32=√1+9+9=√19
|BC|=√(−3)2+(−1)2+12=√9+1+1=√11
Teraz żeby nie myśleć za dużo, to:
https://pl.wikipedia.org/wiki/Wz%C3%B3r_Herona
i z tego mamy pole P.
A wysokość:
 Ja bym jednak zrobil rysunek
gdyż np. jeśli przyjmiemy czarne ozbaczenie to wysokość będzie odlegloscia punktu A od
prostej BC
natomiast jeśli będzie oznaczenie takie jak czerowne to odleglosc punktu A tez będzie
odlegloscia od nowej BC tylko ze nowa BC to stara AC i ma inne równanie
Myle ze wiesz o co chodzi .
Natomiast ja tez mogę się w tym mylic
Ja bym jednak zrobil rysunek
gdyż np. jeśli przyjmiemy czarne ozbaczenie to wysokość będzie odlegloscia punktu A od
prostej BC
natomiast jeśli będzie oznaczenie takie jak czerowne to odleglosc punktu A tez będzie
odlegloscia od nowej BC tylko ze nowa BC to stara AC i ma inne równanie
Myle ze wiesz o co chodzi .
Natomiast ja tez mogę się w tym mylic 
 !
!