proszę o sprawdzenie granicy funkcji z liczbą e.
madzii97: Proszę o sprawdzenie granicy funkcji i g.f. z liczbą e.
| | 3n + 2 | |
lim ( |
| )9n+7 = e3 |
| | 3n + 1 | |
n→
∞
n→
∞
Nie mogę sobie poradzić z twierdzeniem o trzech ciągach, ponieważ z takim się pierwszy raz
spotykam.
lim
n√1+2n−5−n
n→
∞
5 gru 13:54
Janek191:
| | | | 3 n + 2 | |
an = [ ( |
| )3n]3 *( |
| )7 |
| | | | 3 n + 1 | |
więc
| | e2 | |
lim an = ( |
| )3 *1 = e3*1 = e3 |
| | e | |
n→
∞
5 gru 14:00
madzii97: czyli wyszło mi dobrze, proszę o pomoc z 3 przykładem.
5 gru 14:02
Janek191:
więc
| | 0 − 0 | | 0 | |
lim an = |
| = |
| = 0 |
| | 0 + 1 | | 1 | |
n→
∞
5 gru 14:04
madzii97: masz rację, dziękuję.
5 gru 14:08
Janek191:
bn = n√1 + 2n − 15n
Niech
an = n√2n = 2 i cn = n√3 *2n = n√3*2
więc
an ≤ bn ≤ cn
oraz
lim an = 2 i lim cn = 1*2 = 2
n→∞ n→∞
więc na mocy tw. o trzech ciągach
lim bn = 2
n→∞
5 gru 14:09
madzii97: bardzo dziękuje Janek191.
5 gru 14:17
Janek191:

5 gru 14:18
madzii97: Mam jeszcze jedno zadanko do sprawdzenia.
n→4
5 gru 14:24
Janek191:
x → 4
5 gru 14:26
Janek191:
| | x2 − 16 | | ( x − 4)*(x + 4) | |
f(x) = |
| = |
| |
| | I x − 4 I | | I x − 4 I | |
x → 4
− czy x → 4
+
5 gru 14:28
madzii97: x→4
hmm. mam podane tak jak wyżej, nie wiem od której strony 4.
5 gru 14:29
Janek191:
| | ( x − 4)*(x + 4) | |
lim f(x) = lim |
| = lim − (x + 4) = − 8 |
| | − ( x − 4) | |
x→ 4
− x→4
− x→ 4
−
5 gru 14:34
Janek191:
lim f(x) = 8
x→4+
5 gru 14:35
Janek191:
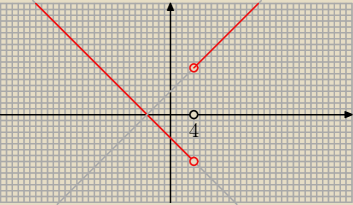
5 gru 14:41

