pochodne
Kacperix: Czy ktos moze mi na tym przykladzie pokazac jak wyznaczac punkty przegiecia funkcji f:
| | −1 | |
f(x)= |
| x3+x2−x+18 , ja pamietma tylko tyle ze trzeba jkaies f bis obliczyc |
| | 3 | |
4 gru 23:44
ax:
f'(x)=−x2+2x−1
f'(x)=0
−(x−1)2=0 ⇒ x=1
jak widzisz pochodna przy przejściu przez ten punkt nie zmienia znaku
Zatem f(x) dla x=1 nie ma ekstremum a punkt przegięcia.
5 gru 00:24
Kacperix: ale jaki pkt przegiecia , w ktora strone sie wygina?
5 gru 15:11
Jerzy:
warunkiem wystarczającym istnienia punktu przegięcia jest zmiana znaku drugiej pochodnej,
ta funkcja nie ma punktu przegięcia
5 gru 15:14
===:
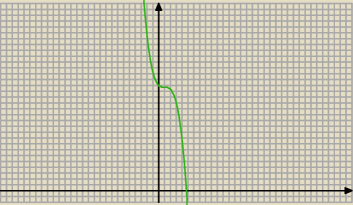
5 gru 15:15
===:
chyba nie bardzo wiesz co mówisz
5 gru 15:16
Jerzy:
druga pochodna zmienia znak ... nie policzyłem , tylko zerknąłem na pierwszą pochodną

5 gru 15:17
===:
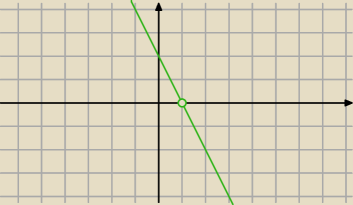
f''(x)=−2x+2x
i jak widać przy przejściu przez x=1 druga pochodna zmienia znak
5 gru 15:19
Jerzy:
@ === ..co masz na mysli ?
5 gru 15:19
===:
już nic
5 gru 15:28
Kacperix: czyli jak rachunkowo przedtsawic w ktora strone sie wygina
5 gru 17:00


 f''(x)=−2x+2x
i jak widać przy przejściu przez x=1 druga pochodna zmienia znak
f''(x)=−2x+2x
i jak widać przy przejściu przez x=1 druga pochodna zmienia znak