geometria analityczna
ppp: Oblicz odległość:
* punktu A(−2,−3) od prostej k:y=x+1
*punktu A(−4,−1) od prostej k:y=0,5x+5
4 gru 21:53
Janek191:
A = ( − 2; − 3)
k : y = x + 1 więc k : x − y + 1 = 0
| | I 1*(−2) + (−1)*(−3) + 1 I | |
d = |
| = |
| | √12 + (−1)2 | |
4 gru 21:57
Janek191:
A x + B y + C = 0
P = (x
o; y
o)
to
| | I A xo + B yo + C I | |
d = |
| |
| | √A2 + B2 | |
4 gru 21:59
ppp: dlaczego x − y + 1 = 0 a nie x+y+1=0?
4 gru 22:01
Janek191:
Bo takie równanie prostej podałaś
y = x + 1
0 = − y + x + 1
0 = x − y + 1
x − y + 1 = 0
=========
4 gru 22:06
ppp: aaa rozumiem
4 gru 22:07
4 gru 22:08
4 gru 22:10
ppp: | | 4 | |
a w tym drugim przykładzie |
| ? |
| | √0,24 | |
4 gru 22:15
Janek191:
A = (− 4; −1)
k : y = 0,5 x + 5 ⇒ 0,5 x − y + 5 = 0 ⇒ x − 2y + 10 = 0
| | I1*(−4) + (− 2)*(−1) + 10 I | | 8 | | 8 √5 | |
d = |
| = |
| = |
| |
| | √12 + (−2)2 | | √5 | | 5 | |
4 gru 22:21
ppp: Dziękuję
4 gru 22:23
ppp: A jeśli chodzi o obliczenie kątu nachylenia y+√3*x−√3
to będzie tak?
y=−√3x+√
a=tgα=√3
α=120º
4 gru 22:29
Janek191:
Przepisz równanie prostej z I wiersza .
y + √3 x − √3 = 0 ?
4 gru 22:32
ppp: y= −√3 x+ √3
4 gru 22:36
ppp: nie wiem,nie umiem
4 gru 22:43
Janek191:
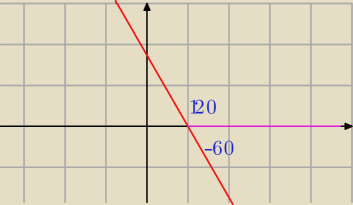
tg α = a = −
√3 ⇒ α = − 60
o + 180
o = 120
o
4 gru 22:45
4 gru 22:47
Janek191:
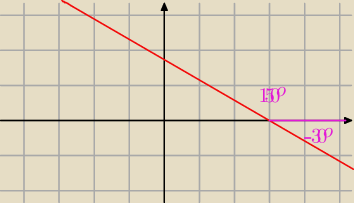
| | √3 | |
tg α = a = − |
| ⇒ α = − 30o + 180o = 150o |
| | 3 | |
4 gru 22:57
ppp: Wielkie dzięki
4 gru 23:00