geometria anlityczna ppp: Oblicz odległość między prostymi k:y −2x−7=0 l: 2x−y+6=0

Janek191: k : − 2 x + y − 7 = 0 / *(−1) ⇒ 2 x − y + 7 = 0 l : 2 x − y + 6 = 0

	I 7 − 6 I		1		√5
d =		=		=
	√ 22 + (−1)2		√5		5

PAULINA5: DANE SA KATYαIβ TROJKATA WPISANEGO W OKRAG O PROMIENIU 6CM NIE KORZYSTAJAC Z TABLIC OBLICZ OBWOD TROJKATA JESLI α=30 β=135

ppp: Oblicz odległość między prostymi k:y −2x−3=0 l: 2x−y−5=0 k:−2x+y−3=0/ * (−1) 2x−y+3=0 l:2x−y−5=0 d= |3+5| przez pierwiastek 2²+(−1)²= ⁸_√5 Dobrze?

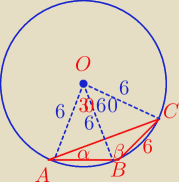
Janek191: α = 30^o ⇒ I ∡ BOC I = 60^o i Δ BCO jest równoboczny. ⇒ I BC I = 6 135^o − 60^o = 75^o I AC I² = 6² + 6² = 2*36 I AC I = 6√2 Z tw. sinusów oblicz I AB I.

ppp: ?

PAULINA5: W ODPOWIEDZIACH JEST 3(2+PIERWIASTEK Z2 +6PIERWIASTEKZ6

Janek191: Albo z tw. cosinusów I ∡ ACB I = 15^o I AB I² = I AC I² + I BC I² − 2*I AC I*I BC I*sin 15^o

ppp: Oblicz odległość między prostymi k:y −2x−3=0 l: 2x−y−5=0 k:−2x+y−3=0/ * (−1) 2x−y+3=0 l:2x−y−5=0 d= |3+5| przez pierwiastek 2²+(−1)²= ⁸_√5=^8√5₅ Dobrze jest to rozwiązane?

Janek191: Gdzie źle policzyłem ?

ppp: To inny przykład

Janek191:

	8		8√5
d =		=
	√5		5

Tak Dlaczego 2 razy piszesz to samo ?

PAULINA5: ROBILAM CALE ZADANIE Z TW SINUSOW I NIE WYCHODZI MI TAK JAK W ODPOWIEDZIACH

ppp: bo zależy mi na czasie,dziękuję