zad proste ja: naszkicuj wykres funkcji g(x)=f(1−x) jezeli: f(x)=

	1		1
dla f(x)=−		x−1 dla x≤−1 oraz		x3 dla x>−1
	2		2

z wykesu odczytaj rozwiazanie nierownosci g(x)≥0

ax: wczoraj było

Hugo:

ja: zrobicie?

ja: jak to zrobic

Borat: Skoro g(x)=f(1−x) to: g(x)=−¹₂(x−1)−1

Borat: −¹₂(1−x)−1 * tak powinno być, sorki

ja: jak mam to niby narysowac chyba trzeba przesunac cos ..nie da sie tego narysowac co podales

Borat: −¹₂(1−x)−1 = ¹₂x−³₂ g(x)=¹₂x−³₂ jest to wykres prostej y=ax+b, więc podstawiasz za x dowolne dwie liczby i zaznaczasz punkty na układzie współrzędnych i rysujesz prostą a następnie ją obcinasz do podanej dziedziny czyli w tym przypadku x≤ −1 i to samo robisz z drugim równaniem a następnie odczytujesz z wykresu to co masz odczytać

ja: jak zrobic to zadanie prosze o pomoc

ja: ze co ? a nie tak ?−−>ja tak zrobilem−−>−1/2(1−x)−1 dla x≤−1 i drugi wzor dla x>−1 ja tak rysuje i wychodzi troche inny wykres a w odp pisze zeby najpierw narysowac wykres f(x)potem f(x−1) a na koniec f(1−x) ale dlaczego jak ja zrobilem to pierwsze to nie wychodzi

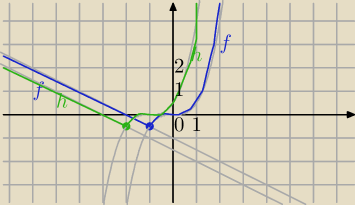
Mila: f(1−x)=f(−x+1) wykres f(x)→Translacja o wektor [−1,0] ⇒otrzymujesz wykres funkcji h(x)=f(x+1)

	1		1		1
h(x)=−		(x+1)−1⇔h(x)=−		x−		−1,
	2		2		2

	1		3
h(x)=−		x−		dla x≤−2
	2		2

	1
h(x)=		(x+1)3 dla x>−2 następnie symetria zielonego wykresu względem OY
	2

otrzymasz wykres g(x)=f(−x+1) Narysuj i napisz wzór, zobacz czy Ci wyjdzie jak w odpowiedzi, po kolacji tu spojrzę. Napisz jak Ci poszło.

ja: zle ci wyszedl wykres powinien byc blize 1 i troche inaczej wyglada

ja: tak powinno wygladac http://uploads.im/kS5T0.jpg

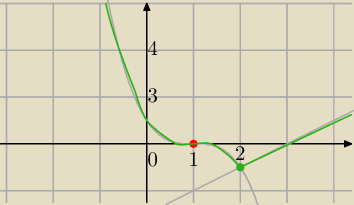
Mila: Ja rozwiązywałam inną metodą, przeczytaj. Zadanie nie jest skończone , jeżeli odbijesz względem OY , to będzie to samo. Ponadto trzeba by dać większe jednostki, aby było dokładniej. Spróbuj zrobić wg mojej instrukcji. Czy wiesz ? 1) jaki jest wzór h(x) =f(x−1) dla obu "gałęzi"? 2) środkowy wykres ( u Ciebie) masz po translacji o wektor [1,0] mojego niebieskiego wykresu. 3) A trzeci wykres to jakie przekształcenie wykonałeś?

ja: translakcja nie mamy tego

Mila: Translacja to inaczej przesunięcie równoległe.

Eta:

Eta: A co to jest : odcięta punktu i rzędna punktu ? wiesz?

Mila: Ja chyba wiem .

Eta:

Eta: Hej "małolatku"

ja: co to ma byc ..ludzie najpierw mi powiedzcie jak to zrobic zwarzajac ze jak podstawie za x 1−x to zle wychodzi a ty mi mowisz o translacji ktorej nie znam

ja: herhor help

Eta: Nie umiemy angielskiego Napisz prośbę w ojczystym języku

Mila: Przecież napisałam. 1) Rysujesz wykres f(x) 2) f(x)→przesunięcie wykresu o wektor [−1,0] ( jedna jednostka w lewo) otrzymujesz wykres funkcji (ten zielony na rys.19:36) h(x)=f(x+1) 3) odbicie symetryczne wykresu h(x) względem osi OY i otrzymujesz wykres g(x)=f(−x+1) ten na wykresie z godziny 23:00 Ponadto zadajesz grzecznie pytanie, jeżeli masz wątpliwości. Po co te nerwy, my się nie denerwujemy, tym, że ktoś czegoś nie rozumie.

Mila: Eta zobacz ten rysunek w linku,

ja: ej gdzie jest linki nie ma linku

Mila: do Ja, napisz jakie wzory, czy wykresy Ci nie wychodzą.

Mila: 19:47, to było do Ety

Mila: To do jutra. Dobranoc

ja: no jak za x podstawie 1−x to ne wychodzi

Mila: Jutro, wyjaśnię po kolei , bo teraz zasypiam.

ja: bywaj

ja: slucham

ja: dziukasi pomozcie

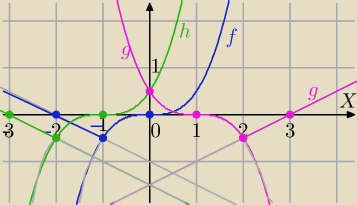
Mila: Wiadomości: a) Po przesunięciu wykresu funkcji f(x) o wektor [a,0] otrzymujesz wykres funkcji o wzorze f(x−a), czyli po przesunięciu o wektor [−1,0] wzór f(x−(−1))=f(x+1) b) po odbiciu symetrycznym wykresu f(x) względem OY otrzymujesz wykres funkcji o wzorze f(−x) ================= W tym rozwiązaniu w książce masz zastosowane przekształcenia: 1) przesunięcie o wektor [1,0] i otrzymasz wzór funkcji:

	1		1		1
f(x−1)=−		(x−1)−1=−		x+		−1 ⇔
	2		2		2

	1		1
f(x−1)= −		x−		dla x≤0
	2		2

i

	1
f(x−1)=		(x−1)) 3 dla x>0
	2

2) Następnie masz zastosowaną symetrię względem prostej x=1 i tu już trzeba zastosować pewne wzory, nie wiem, czy to umiesz, dlatego zaproponowałam inny sposób, wtedy łatwo napisac wzory. bo łatwo pisać wzory. ================== Możesz od razu obliczyć jaki jest wzór końcowy ( nie przejmując się środkowym wykresem) tak:

	1		1		3
g(x)=−		(−x+1)−1⇔g(x)=		x−
	2		2		2

	1
g(x)=		(−x+1)3
	2

Dla jakich x−ów ustalasz wg wykresu. ============================ Jesteś w LO , czy na studiach? Bo nie wiem na jakim poziomie to tłumaczyć. wg mojej motody: 1) Przesunięcie wykresu f(x) o wektor [−1,0] , otrzymasz wzór:

	1		1		3
h(x)=f(x+1)=−		(x+1)−1=−		x−		dla x≤−2
	2		2		2

	1
h(x)=		(x+1)3 dla x>2
	2

2) symetria względem OY otrzymujesz wzory:

	1		3
g(x)=		x−		dla x≥2
	2		2

	1
g(x)=		(−x+1)3 dla x<2
	2

================== g(x)≥0 ⇔x∊(−∞, 1>∪<3,∞) =============== Wykresy popielate nie są brane pod uwagę ( to linie pomocnicze, tutaj nie można narysować kawałka wykresu, dlatego zamazałam)

ja: bez jaj to jest zad z matury rozszerzonej ale...

ja: dziekuje bynajmniej bardzo

ja: nic z tego nie rozumiem o co tu wogole chodzi

ja: dlaczego sie przesuwa w prawo a nie w lewo