przekształcanie hajdik: naszkicuj wykres funkcji f(x)= 1/2(|x|−2)²−1 oraz g(x)= |2(x+3)²−2|.. Nie mam pojęcia jak to rozpisać i poźniej narysować.. Proszę o pomoc

J: f(x):

	1
dla x ≥ 0 f(x) =		(x−2)2 − 1
	2

	1
dla x < 0 f(x) =		(−x−2)2 − 1
	2

g(x) ... rysujesz : g(x) = 2(x+3)² − 2 , potem to co pod osią OX odbijasz nad oś

hajdik: a przedział monotoniczności dla f(x) dla x≥0 jest funkcja malejąca (−∞,2> i rosnąca dla <2.∞) a dla x<0 ? a g(x) będzie malejąca (−∞,−3> i rosnąca<3,∞) ?

Marta: ?

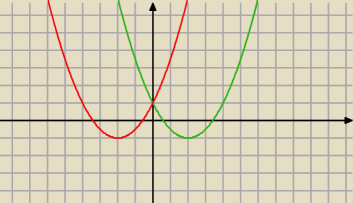
J: teraz ustalaj przedziały monotoniczności

J: rysunek dotyczy oczywiście tylko funkcji f(x) : czerwony dla x < 0 , zielony dla x ≥ 0

Marta: a to nie jest tak, że wierzchołek f(x) jest równe 2 a nie −2?

Marta: oczywiście pierwsza wspołrzędna. Czyli W=(2,−1)

J: y_w = −1 ( popatrz na wykres )

J: nie widzisz,że ta funkcja ma dwa wierzchołki: x_w = − 2 oraz x_w = 2

Marta: ah, sorry. faktycznie

hajdik: g(x) będzie miało monotniczność : maleje (−∞,2> i rośnie od <2,∞) ?

J: a gdzie ma wierzchołek ?

hajdik: wierzchołek ma w (−3,−2) ale na początku było napisane, ze mam cos odbić, hmm

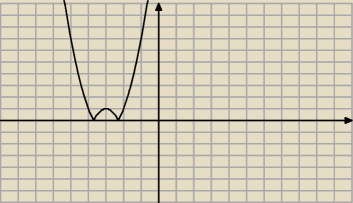
J: zapomniałem teraz ustalaj

hajdik: czyli maleje od (−∞, −4> oraz <−3,−2> i rośnie od <−4,−3> oraz <−2,∞> tak?

natalia: dobrze rozumuje?

J: rozumowanie jest dobre .. tylko miejsca zerowe chyba złe

hajdik: bardzo Cie prosze, pomóż mi w takim razie wyznaczyć ta monotoniczność .

J: oblicz miejsca zerowe tej funkcji

hajdik: miejsca zerowe to −4 i −2

hajdik: i co dalej?

J: 10:47 ... masz OK ... to ja się pomyliłem

hajdik: to dziękuję w takim razie pozdrawiam