fkcje kwadratowa dowodhelp: Funkcja kwadratowa. Obwód pewnego trójkąta jest równy 6 cm, a jeden z jego kątów ma miarę 60 stopni. Promień okręgu

	2√3
opisanego na tym trójkącie ma długości R =		cm. Wyznacz długości boków tego
	3

trójkąta tak, aby jego pole było największe. Oblicz pole trójkąta dla wyznaczonych długości boków. Zrobiłem to zadanie podstawiając pod wzór z promieniem okręgu opisanego na trójkącie zawierającym sinus α, lecz nie mam pomysłu jak opisać to za pomocą funkcji kwadratowej.. ktoś mógłby pomóc?

dowodhelp: UP.

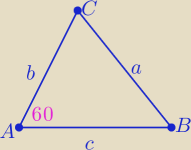
Eta: Z tw. sinusów :

a		2√3		√3
	=2R ⇒ a=2*		*		= 2
sin60o		3		2

a+b+c=6 ⇒ b+c=4 ⇒ b= 4−c i c∊(0,4)

	1		√3		√3
P=		b*c*sin60o =		*c(4−c) = −		c2+√3c
	2		4		4

parabola ramionami do góry

	−√3
to cmax=		= 2
	√3   2*(− )   4

to b_max= 4−2= 2 Takim trójkątem o największym polu jest trójkąt równoboczny o boku długości 2

	22√3
PΔ=		= √3 [j2]
	4

dowodhelp: Bardzo bardzo bardzo dziękuję.

Eta:

Eta: Poprawiam chochlika Oczywiście ma być : parabola ramionami do dołu