trudne dziedzina Krzysiek: cześć mam takie zadanie określić dziedzinę

	ln(cos22x − 12)
f(x) =
	√tg3x − 1 + tg2x − tgx

robię założenia : 1 : tg³x − 1 + tg²x − tgx ≥ 0 2 : cos²2x − ¹₂ > 0 3 : √tg³x − 1 + tg²x − tgx czy to trzecie założenie jest ok? 1 : po przekształceniach wychodzę na takie coś (tgx − 1)(tgx + 1)(tgx + 1) ≥ 0 tgx = 1 ⋁ tgx = −1 ⋁ tgx = −1 nie wiem jak teraz zrobić do tego przedział, jaką dać odpowiedź ==================================================== 2 :

	1
(2cos2x −1)2 −		> 0
	2

	√2		√2
(2cos2x −1 −		)(2cos2x −1 +		) > 0 czy ta linijka jest dobrze?
	2		2

jak dalej co ciągnąć ....

Krzysiek:

Mila:

	π
W (1) dołożyć x≠		+kπ, i ma być (>0), bo mianownik różny od zera.
	2

2)

	1
cos2x−		>0
	2

	1
cos2x>		⇔
	2

	√2
|cosx|>		⇔
	2

	√2		√2
cosx>		lub cosx<−
	2		2

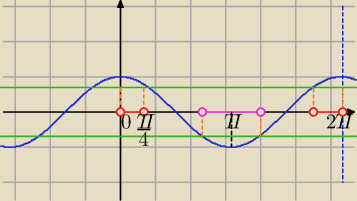
odczytuj

Mila: (tgx − 1)(tgx + 1)(tgx + 1) > 0 (t−1)*(t+1)²>0⇔ (t+1)²>0 dla t∊D t>1⇔ tg(x)>1

	π		π
x∊(		+kπ,		+kπ)
	4		2

Krzysiek: skąd w drugim takie coś się zrobiło ?

Mila: (2)

	1
cos2(2x)>
	2

Powinnam napisać 2x=t

	1
cos2(t)>
	2

Rozwiązałam dla cos (t), możesz łatwo odczytać przedziały. ( nie zmieniłam nazwy argumentu i to jest mylące.)

	π		3π		5π		7π
0+2kπ<2x<		+2kπ lub U{		+2kπ<2x<		+2kπ lub		+2kπ<2x<2π+2kπ /:2
	4		4		4		4

	π		3π		5π		7π
0+kπ<2x<		+kπ lub		+kπ<x<		+kπ lub		+kπ<x<π+kπ
	8		8		8		8

Krzysiek: dziękuję

Mila: